Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) \(a^5-a=a\left(a^4-1\right)=a\left(a^2-1\right)\left(a^2+1\right)\)
\(=\left(a-1\right)a\left(a+1\right)\left(a^2-4+5\right)\)
\(=\left(a-1\right)a\left(a+1\right)\left(a^2-4\right)+5\left(a-1\right)a\left(a+1\right)\)
\(=\left(a-2\right)\left(a-1\right)a\left(a+1\right)\left(a+2\right)+5\left(a-1\right)a\left(a+1\right)⋮5\)
Vì \(\left(a-2\right)\left(a-1\right)a\left(a+1\right)\left(a+2\right)⋮5\)( tích 5 số nguyên liên tiếp chia hết cho 5)
và \(5\left(a-1\right)a\left(a+1\right)⋮5\)
=> \(a^5-a⋮5\)
Nếu \(a^5⋮5\)=> a chia hết cho 5

Do \(p\) là số nguyên tố \(>3\) nên :
\(\Rightarrow\left[{}\begin{matrix}p=6k+1\\p=6k+5\end{matrix}\right.\) \(\left(k\in N\right)\)
+) Với \(p=6k+5\) thì :
\(p+4=\left(6k+5\right)+4=6k+9⋮3\) \(\left(loại\right)\) \(\rightarrow\) Do \(p+4\) là số nguyên tố
\(\Rightarrow p=6k+1\).Vậy khi đó :
\(p+8=\left(6k+1\right)+8=6k+9⋮3\) (thỏa mãn \(p+8\) là hợp số )
\(\Rightarrowđpcm\)
~ Học tốt ~

Đáp án: D
P: “n là một số nguyên tố lớn hơn 3”; Q: “n2 + 20 là một hợp số”.
Mệnh đề đã cho: P => Q. Nghĩa là, Điều kiện đủ để có Q là P hay Điều kiện cần để có P là Q. Do đó B, C đúng

8x2 hoặc bằng 0 hoặc có ước là 8 => Không có x nào thỏa mãn bài toán


vì \(2^n-1\) là số nguyên tố nên tổng các ước của \(2^n-1\) là \(1+2^n-1\)
tổng các ước của \(2^{n-1}\left(2^n-1\right)\) là \(\displaystyle\Sigma ^{n-1}_{i=0}(2^i)\times (1+2^n-1)\)\(=\left(2^n-1\right)\times2^n=2\left[2^{n-1}\left(2^n-1\right)\right]\)
Vậy số đã cho là số hoàn hảo



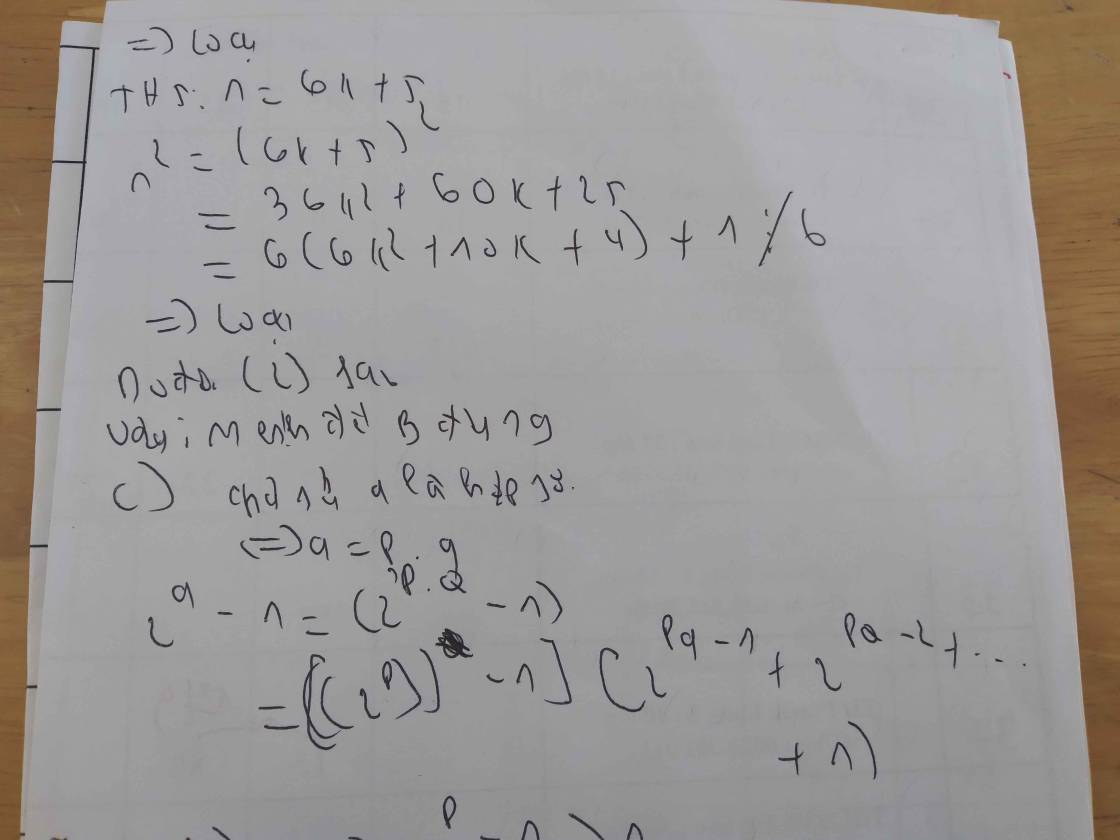

Do P là số nguyên tố
TH1:P chia 3 dư 1
=>P=3k+1(k là số tự nhiên)
2P+1=6k+2+1=6k+3 chia hết cho 3
Mà 2P+1 là số nguyên tố nên loại
TH2:P chia 3 dư 2
=>P=3k+2(k là số tự nhiên)
=>2P+1=6k+5(thõa mãn P là số nguyên tố)
=>4P+1=12k+9 chia hết cho 3
=>4P+1 là hợp số
=>đpcm