Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(\frac{A}{2}+\left(\frac{B}{2}+\frac{C}{2}\right)=90^0\)
\(\Rightarrow sin\frac{A}{2}=cos\left(\frac{B}{2}+\frac{C}{2}\right)=cos\frac{B}{2}cos\frac{C}{2}-sin\frac{B}{2}.sin\frac{C}{2}\)
b/ \(\frac{tan^2A-tan^2B}{1-tan^2A.tan^2B}=\frac{\left(tanA-tanB\right)}{\left(1+tanA.tanB\right)}.\frac{\left(tanA+tanB\right)}{\left(1-tanA.tanB\right)}=tan\left(A-B\right).tan\left(A+B\right)\)
\(=tan\left(A-B\right).tan\left(180^0-C\right)=-tan\left(A-B\right).tanC\)
c/
\(A+B+C=180^0\Rightarrow cot\left(A+B\right)=-cotC\)
\(\Leftrightarrow\frac{cotA.cotB-1}{cotA+cotB}=-cotC\)
\(\Leftrightarrow cotA.cotB-1=-cotA.cotC-cotB.cotC\)
\(\Leftrightarrow cotA.cotB+cotB.cotC+cotA.cotC=1\)

Lời giải:
a)
\(\frac{\sin ^2a+2\cos ^2a-1}{\cot ^2a}=\frac{(\sin ^2a+\cos ^2a)+\cos ^2a-1}{\cot ^2a}=\frac{1+\cos ^2a-1}{\cot ^2a}=\frac{\cos ^2a}{\cot ^2a}=\frac{\cos ^2a}{(\frac{\cos a}{\sin a})^2}=\sin ^2a\)
b)
\(\frac{1-\sin ^2a\cos ^2a}{\cos ^2a}-\cos ^2a=\frac{1}{\cos ^2a}-\sin ^2a-\cos ^2a\)
\(=\frac{\sin ^2a+\cos ^2a}{\cos ^2a}-(\sin ^2a+\cos ^2a)=\tan ^2a+1-1=\tan ^2a\)
c)
\(\frac{\sin ^2a-\tan ^2a}{\cos ^2a-\cot ^2a}=\frac{\sin ^2a-\frac{\sin ^2a}{\cos ^2a}}{\cos ^2a-\frac{\cos ^2a}{\sin ^2a}}=\frac{\sin ^4a(\cos ^2a-1)}{\cos ^4a(\sin ^2a-1)}\)
\(=\frac{\sin ^4a(-\sin ^2a)}{\cos ^4a(-\cos ^2a)}=\frac{\sin ^6a}{\cos ^6a}=\tan ^6a\)

\(cos^4a+sin^4a-6sin^2a.cos^2a\)
\(=cos^4a+sin^4a-2sin^2a.cos^2a-4sin^2a.cos^2a\)
\(=\left(cos^2a-sin^2a\right)^2-\left(2sina.cosa\right)^2\)
\(=cos^22a-sin^22a\)
\(=cos4a\)

\(A+B+C=180^0\Rightarrow\frac{A}{2}+\frac{B}{2}+\frac{C}{2}=90^0\Rightarrow\frac{A}{2}+\frac{B}{2}=90^0-\frac{C}{2}\)
\(\Rightarrow tan\left(\frac{A}{2}+\frac{B}{2}\right)=tan\left(90^0-\frac{C}{2}\right)\)
\(\Leftrightarrow\frac{tan\frac{A}{2}+tan\frac{B}{2}}{1-tan\frac{A}{2}.tan\frac{B}{2}}=cot\frac{C}{2}=\frac{1}{tan\frac{C}{2}}\)
\(\Leftrightarrow tan\frac{C}{2}\left(tan\frac{A}{2}+tan\frac{B}{2}\right)=1-tan\frac{A}{2}.tan\frac{B}{2}\)
\(\Leftrightarrow tan\frac{A}{2}tan\frac{C}{2}+tan\frac{B}{2}tan\frac{C}{2}+tan\frac{A}{2}.tan\frac{B}{2}=1\)
b/\(A+B+C=180^0\Rightarrow A+B=180^0-C\)
\(\Rightarrow cot\left(A+B\right)=cot\left(180^0-C\right)\)
\(\Leftrightarrow\frac{cotA.cotB-1}{cotA+cotB}=-cotC\)
\(\Leftrightarrow cotA.cotB-1=-cotA.cotC-cotB.cotC\)
\(\Leftrightarrow cotA.cotB+cotB.cotC+cotA.cotC=1\)
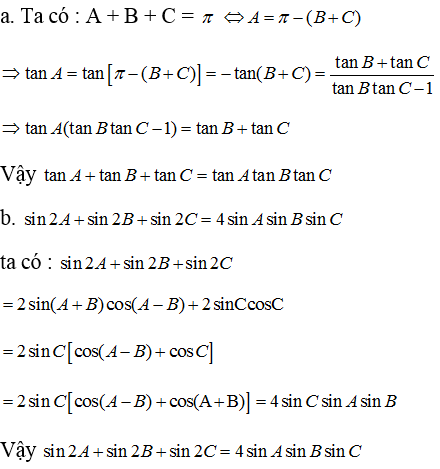
\(A+B+C=180^0\Rightarrow tan\left(A+B\right)=-tanC\)
\(\Rightarrow\frac{tanA+tanB}{1-tanA.tanB}=-tanC\Leftrightarrow tanA+tanB=-tanC+tanA.tanB.tanC\)
\(\Leftrightarrow tanA+tanB+tanC=tanA.tanB.tanC\)
\(2A+2B+2C=360^0\Rightarrow tan\left(2A+2B\right)=-tan2C\)
\(\Leftrightarrow\frac{tan2A+tan2B}{1-tan2A.tan2B}=-tan2C\)
\(\Leftrightarrow tan2A+tan2B+tan2C=tan2A.tan2B.tan2C\)