Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H
a) Xét tam giác ABH và tam giác ACH có
AB=AC (tam giác ABC cân tại A)
\(\widehat{ABH}=\widehat{ACH}\)(tam giác ABC cân tại A)
BH=HC(H là trung điểm BC)
=> Tam giác ABH = Tam giác ACH (cgc)
b) Vì tam giác ABC cân tại A (gt) và H là trung điểm BC(gt)
=> AH là đường trung tuyến đồng thời là đường cao của tam giác ABC
=> AH vuông góc với BC(đpcm)
A C B H E K 1 2
a) Xét t/giác ABH và t/giác ACH
c: AB = AC (gt)
BH = CH (gt)
AH: chung
=> t/giác ABH = t/giác ACH (c.c.c)
b) Ta có: t/giác ABH = t/giác ACH (cmt)
=> \(\widehat{AHB}=\widehat{AHC}\)(2 góc t/ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(kề bù)
=> \(\widehat{AHB}=\widehat{AHC}=90^0\)
=> AH \(\perp\)BC
c) Ta có: BH = CH = 1/BC = 1/2.6 = 3 (cm)
Áp dụng định lí Pi - ta - go vào t/giác ABH vuông tại H, ta có:
AB2 = AH2 + BH2 => AH2 = 52 - 32 = 16
=> AH = 4 (cm)
d) Ta có: t/giác AHB = t/giác AHC (cmt)
=> \(\widehat{A_1}=\widehat{A_2}\) (2 góc t/ứng)
Xét t/giác AHE và t/giác AHK
có: \(\widehat{A_1}=\widehat{A_2}\)(cmt)
AH : chung
\(\widehat{AEH}=\widehat{AKH}=90^0\)(gt)
=> t/giác AHE = t/giác AHK (ch - gn)
=> HE = HK (2 cạnh t/ứng)
e) Ta có: t/giác AHE = t/giác AHK (cmt)
=> AE = AK (2 cạnh t/ứng)
=> t/giác AEK cân tại A
=> \(\widehat{AEK}=\widehat{AKE}=\frac{180^0-\widehat{A}}{2}\)(1)
T/giác ABC cân tại A
=> \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\)(2)
Từ (1) và (2) => \(\widehat{AEK}=\widehat{B}\)
Mà 2 góc này ở vị trí đồng vị
=> EK // BC

a,xét tam giác ABH và tam giác ACH co
BH=HC(gt)
AH CHUNG
A1=A2=>TAM GIAC ABH=TM GIAC ACH
C,

a: Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH

a, xét tam giác AHB và tg AHC có : ^AHC = ^AHB = 90
AB = AC do tg ABC cân tại A (gt)
^ABC = ^ACB do tg ABC ...
=> tg AHB = tg AHC (ch-gn)
b, tg ABC cân tại A (Gt) mà có AH là đường cao (1)
=> AH đồng thời là đường trung tuyến
=> H là trung điểm của BC
=> BH = 1/2BC = 6 cm
tg AHB vuông tại H (gt) => AB^2 = AH^2 + HB^2 (ĐL pytago)
AB = 10 (gt)
=> AH = 8 do AH > 0
c, (1) => AH đồng thời là pg của ^BAC (đl)
=> ^CAH = ^BAH (đn)
có HE // AC (gt) ; ^CAH slt ^AHE => ^CAH = ^AHE (đl)
=> ^BAH = ^AHE
=> tg AHE cân tại E (dh)
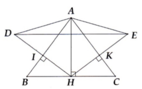



a: Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>\(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
=>AH\(\perp\)BC
c: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA=\sqrt{5^2-3^2}=4\left(cm\right)\)
d: ΔAHB=ΔAHC
=>\(\widehat{HAB}=\widehat{HAC}\)
Xét ΔAEH vuông tại E và ΔAKH vuông tại K có
AH chung
\(\widehat{EAH}=\widehat{KAH}\)
Do đó: ΔAEH=ΔAKH
=>HE=HK
e: ΔAEH=ΔAKH
=>AE=AK
Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AK}{AC}\)
nên EK//BC