Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi điểm cố định mà các đường thẳng (d) đều đi qua P( x o , y o ).
Ta có:
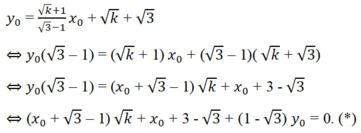
Phương trình (*) nghiệm đúng với mọi giá trị không âm của k , do đó ta có:
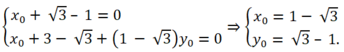
Vậy, với k ≥ 0, các đường thẳng (d) đều đi qua điểm cố định P(1- 3 ; 3 – 1).

Với k ≥ 0 ta có:
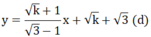
Giả sử ( x 0 ; y 0 ) là điểm cố định mà (d) luôn đi qua
Khi đó ta có:
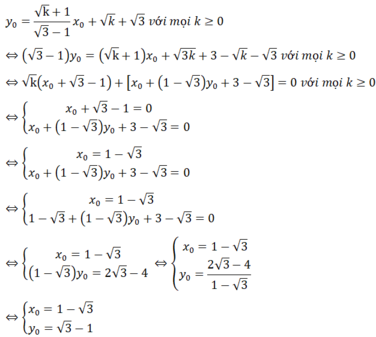
Vậy điểm cố định mà (d) luôn đi qua với mọi k ≥ 0 là (1- 3 ; 3 -1)

a) (d) đi qua điểm (1;2)
<=> 2 = k + 1 + k
<=> 1 = 2k
<=> k = 0,5
Vậy k = 0,5 thì (d) đi qua (1;2)
b) Để (d) // đgth y = 2x + 3
\(\Leftrightarrow\hept{\begin{cases}k+1=2\\k\ne3\end{cases}\Leftrightarrow\hept{\begin{cases}k=1\\k\ne3\end{cases}\Rightarrow}k=1}\)
Vậy k =1 thì (d) // đgth y = 2x +3
c) Gọi điểm cố định là (d) đi qua là (x0;y0)
Ta có y0 = ( k +1) x0 + k
<=> y0 = kx0 + x0+k
<=> y0 - x0 - k ( x0 + 1) = 0 \(\forall\)k
Để pt nghiệm đúng với mọi k <=> \(\hept{\begin{cases}x_0+1=0\\y_0-x_0=0\end{cases}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=-1\end{cases}}}\)
Điểm cố định (d) luôn đi qua là ( -1;-1)

Gọi điểm cố định là \(M\left(x_0;y_0\right)\)
\(\Rightarrow2mx_0+2m+1=y_0\) \(\left(\forall m\right)\)
\(\Leftrightarrow2m\left(x_0+1\right)=y_0-1\) \(\left(\forall m\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0+1=0\\y_0-1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=1\end{matrix}\right.\)
Vậy đường thẳng luôn đi qua \(M\left(-1;1\right)\)

a:
Sửa đề: \(I\left(\dfrac{1}{2};-3\right)\)
Thay \(x=\dfrac{1}{2};y=-3\) vào (d): \(y=\left(1-2m\right)x+m-\dfrac{7}{2}\), ta được:
\(\left(1-2m\right)\cdot\dfrac{1}{2}+m-\dfrac{7}{2}=-3\)
=>\(\dfrac{1}{2}-m+m-\dfrac{7}{2}=-3\)
=>\(\dfrac{1}{2}-\dfrac{7}{2}=-3\)
=>-3=-3(đúng)
vậy: I(1/2;-3) là điểm cố định mà (d): \(y=\left(1-2m\right)x+m-\dfrac{7}{2}\) luôn đi qua
b: \(\left(d\right):y=\left(2m+1\right)x+m-2\)
\(=2mx+x+m-2\)
\(=m\left(2x+1\right)+x-2\)
Điểm mà (d) luôn đi qua có tọa độ là:
\(\left\{{}\begin{matrix}2x+1=0\\y=x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{1}{2}-2=-\dfrac{5}{2}\end{matrix}\right.\)

y=mx+2x-m+3=m(x-1)+2x+3
ĐIểm mà d luôn đi qua là:
x-1=0 và y=2x+3
=>x=1 và y=2+3=5
a/ Gọi điểm cố định \(M\left(x_0;y_0\right)\)
Khi đó đường thẳng y = k(x+3)-7 đi qua M , tức \(k\left(x_0+3\right)-7-y_0=0\)
Vì đường thẳng y = k(x+3)-7 luôn đi qua M nên \(\hept{\begin{cases}x_0+3=0\\-y_0-7=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x_0=-3\\y_0=-7\end{cases}}\)
Vậy đường thẳng đã cho luôn đi qua điểm M(-3;-7)
b/ Gọi điểm cố định là \(N\left(x_0;y_0\right)\)
Vì họ đường thẳng (m+2)x + (m-3)y -m+8 = 0 luôn đi qua N nên :
\(\left(m+2\right).x_0+\left(m-3\right).y_0-m+8=0\)
\(\Leftrightarrow m\left(x_0+y_0-1\right)+\left(2x_0-3y_0+8\right)=0\)
Ta có \(\hept{\begin{cases}x_0+y_0-1=0\\2x_0-3y_0+8=0\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=2\end{cases}}\)
Vậy điểm cố định N(-1;2)
Câu còn lại bạn làm tương tự nhé ^^
c/ Đơn giản thôi mà =)
Ta cũng gọi điểm cố định đó là \(M\left(x_0;y_0\right)\)
Vì họ đường thẳng y=(2-k)x+k-5 đi qua M nên :
\(y_0=\left(2-k\right)x_0+k-5\Leftrightarrow k\left(1-x_0\right)+\left(2x_0-y_0-5\right)=0\)
Ta có \(\hept{\begin{cases}1-x_0=0\\2x_0-y_0-5=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x_0=1\\y_0=-3\end{cases}}\)
Vậy điểm cố định là M(1;-3)