Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta\)ABC vg tại A , ad tỉ số lg giác trong tg vg ta có
a,\(\sin^2\alpha+\cos^2\alpha\)=\(\frac{AB^2}{BC^2}\)+ \(\frac{AC^2}{BC^2}\)= \(\frac{BC^2}{BC^2}\)=1
b,\(\frac{\sin\alpha}{\cos\alpha}\)= \(\frac{AB}{BC}\): \(\frac{AC}{BC}\)= \(\frac{AB}{AC}\)= \(\tan\alpha\)
#mã mã#

Hướng dẫn giải:
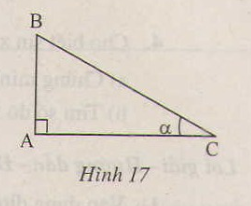
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khá
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.

Lên mạng search ik! Vào Vietjack hay Loigiaihay đều có hết. :)

a/ \(\sin\alpha=\frac{C_đ}{C_h}\)
\(\cos\alpha=\frac{C_k}{C_h}\)
\(\Rightarrow\frac{\sin\alpha}{\cos\alpha}=\frac{\frac{C_đ}{C_h}}{\frac{C_k}{C_h}}=\frac{C_đ}{C_k}=\tan\alpha\)
b/ \(\frac{\cos\alpha}{\sin\alpha}=\frac{\frac{C_k}{C_h}}{\frac{C_đ}{C_h}}=\frac{C_k}{C_đ}=\cot\alpha\)
c/ \(\tan\alpha.\cot\alpha=\frac{C_đ}{C_k}.\frac{C_k}{C_đ}=1\)
d/ \(\sin^2\alpha=\frac{C_đ^2}{C_h^2}\)
\(\cos^2\alpha=\frac{C_k^2}{C_h^2}\)
\(\Rightarrow\sin^2\alpha+\cos^2\alpha=\frac{C_đ^2+C_k^2}{C_h^2}=\frac{C_h^2}{C_h^2}=1\)
P/s: hok trc lp 9 hay sao mà lm bài bài này?

tớ mới tham gia nên k biết viết anpha,tớ sẽ viết là @ nhé.hình vẽ là tam giác ABC có Bc và cạnh huyền,AB là cạnh kề còn AC là cạnh đối(tớ cho góc B làm góc anpha)
a,tan@=AC/AB
sin@=AC/BC (1),cos@=AB/BC (2)
từ (1) và (2) suy ra sin@/cos@=AC/BC : AB/BC = AC/BC x BC/AB= AC/AB
mà tan@ = AC/AB
=>tan@=sin@/cos@
những câu sau làm tương tự nhé

a) \(\frac{1-\cos\alpha}{\sin\alpha}=\frac{\sin\alpha}{1+\cos a}\)
\(\Leftrightarrow\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)=\sin^2\alpha\)
\(\Leftrightarrow1-\cos^2\alpha=\sin^2\alpha\)
\(\Leftrightarrow\sin^2\alpha+\cos^2\alpha=1\)( luôn đúng )
\(\Rightarrow\frac{1-\cos\alpha}{\sin\alpha}=\frac{\sin\alpha}{1+\cos\alpha}\)

\(\frac{\cos a-\sin a}{cosa+sina}=\frac{\frac{cosa}{cosa}-\frac{sina}{cosa}}{\frac{cosa}{cosa}+\frac{sina}{cosa}}\)(chia ca tu va mau cho cosa)
\(=\frac{1-tana}{1+tana}=vt\left(dpcm\right)\)

1) \(1-2\sin\alpha.\cos\alpha=\sin^2\alpha-2\sin\alpha.\cos\alpha+\cos^2\alpha=\left(\sin\alpha-\sin\alpha\right)^2\ge0\)
2) \(\frac{\cos\alpha-\sin\alpha}{\cos\alpha+\sin\alpha}=\frac{1-\frac{\sin\alpha}{\cos\alpha}}{1+\frac{\sin\alpha}{\cos\alpha}}=\frac{1-\tan\alpha}{1+\tan\alpha}=\frac{1-\frac{1}{2}}{1+\frac{1}{2}}=\frac{1}{3}\)
\(\frac{\cos\alpha-\sin\alpha}{\cos\alpha+\sin\alpha}=\frac{\frac{\cos\alpha}{\sin\alpha}-1}{\frac{\cos\alpha}{\sin\alpha}+1}=\frac{\cot\alpha-1}{\cot\alpha+1}=\frac{\frac{1}{\tan\alpha}-1}{\frac{1}{\tan\alpha}+1}=\frac{\frac{1}{\frac{1}{2}}-1}{\frac{1}{\frac{1}{2}}+1}=\frac{1}{3}\)