Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Bài toán trọng tâm của tứ diện:
A B C D G E F H K M N
Ta có NE,MF lần lượt là đường trung bình của \(\Delta ABC,\Delta ADC\), suy ra \(\hept{\begin{cases}NE=MF=\frac{AC}{2}\\NE||MF\end{cases}}\)
Suy ra tứ giác EMFN là hình bình hành. Do đó EF,MN cắt nhau tại trung điểm của mỗi đoạn.
Tương tự MN,HK cũng cắt nhau tại trung điểm của mỗi đoạn.
Vậy EF,HK,MN đồng quy tại trung điểm G của chúng. G chính là trọng tâm của tứ diện ABCD.
*) Nhận xét: Ta dễ dàng chỉ ra:
i) AG,BG,CG,DG lần lượt đi qua trọng tâm GA,GB,GC,GD của các tam giác BCD,ACD,ABD,AB
ii) \(\frac{GA}{GG_A}=\frac{GB}{GG_B}=\frac{GC}{GG_C}=\frac{GD}{GG_D}=3\)
iii) \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\)
2) Ta phát biểu bổ đề sau: Cho tam giác ABC, điểm M thuộc đường thẳng BC. Ta có \(\overrightarrow{AM}=\frac{\overline{BM}}{\overline{BC}}\overrightarrow{AC}+\frac{\overline{CM}}{\overline{CB}}\overrightarrow{AB}\)
A B C M N
Chứng minh: Lấy điểm N trên AB sao cho MN || AC, ta có:
\(\overrightarrow{AM}=\overrightarrow{AN}+\overrightarrow{NM}=\frac{\overline{AN}}{\overline{AB}}\overrightarrow{AB}+\frac{\overline{NM}}{\overline{AC}}\overrightarrow{AC}=\frac{\overline{CM}}{\overline{CB}}\overrightarrow{AB}+\frac{\overline{BM}}{\overline{BC}}\overrightarrow{AC}\)
Lời giải:
A B C D A' B' C' D' G A G
Gọi G và G' lần lượt là trọng tâm của tứ diện ABCD và A'B'C'D'.
Ta có: \(\overrightarrow{AG}=\frac{3}{4}\overrightarrow{AG_A}=\frac{3}{4}.\frac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)=\frac{\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}}{4}\left(1\right)\)
Mặt khác \(\frac{\overline{A'A}}{\overline{A'B}}=\frac{\overline{B'B}}{\overline{B'C}}=\frac{\overline{C'C}}{\overline{C'D}}=\frac{\overline{D'D}}{\overline{D'A}}=k\), suy ra:
\(\frac{\overline{AA'}}{\overline{AB}}=\frac{\overline{BB'}}{\overline{BC}}=\frac{\overline{CC'}}{\overline{CD}}=\frac{k}{k-1};\frac{\overline{AD'}}{\overline{AD}}=\frac{\overline{DC'}}{\overline{DC}}=\frac{\overline{CB'}}{\overline{CB}}=\frac{-1}{k-1}\)
Từ đó: \(\overrightarrow{AA'}=\frac{\overline{AA'}}{\overline{AB}}\overrightarrow{AB}=\frac{k}{k-1}\overrightarrow{AB};\overrightarrow{AD'}=\frac{-1}{k-1}\overrightarrow{AD}\)
\(\overrightarrow{AB'}=\frac{\overline{BB'}}{\overline{BC}}\overrightarrow{AC}+\frac{\overline{CB'}}{\overline{CB}}\overrightarrow{AB}=\frac{k}{k-1}\overrightarrow{AC}-\frac{1}{k-1}\overrightarrow{AB}\)
\(\overrightarrow{AC'}=\frac{\overline{CC'}}{\overline{CD}}\overrightarrow{AD}+\frac{\overline{DC'}}{\overline{DC}}\overrightarrow{AC}=\frac{k}{k-1}\overrightarrow{AD}-\frac{1}{k-1}\overrightarrow{AC}\)
Suy ra \(\overrightarrow{AG'}=\frac{1}{4}\left(\overrightarrow{AA'}+\overrightarrow{AB'}+\overrightarrow{AC'}+\overrightarrow{AD'}+\overrightarrow{A'G'}+\overrightarrow{B'G'}+\overrightarrow{C'G'}+\overrightarrow{D'G'}\right)\)
\(=\frac{\overrightarrow{AA'}+\overrightarrow{AB'}+\overrightarrow{AC'}+\overrightarrow{AD'}}{4}\)
\(=\frac{1}{4}\left(\frac{k}{k-1}\overrightarrow{AB}+\frac{k}{k-1}\overrightarrow{AC}-\frac{1}{k-1}\overrightarrow{AB}+\frac{k}{k-1}\overrightarrow{AD}-\frac{1}{k-1}\overrightarrow{AC}-\frac{1}{k-1}\overrightarrow{AD}\right)\)
\(=\frac{\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}}{4}\left(2\right)\)
Từ (1),(2) suy ra \(\overrightarrow{AG}=\overrightarrow{AG'}\). Vậy G trùng G' hay hai tứ diện ABCD và A'B'C'D' có cùng trọng tâm.

Gọi M. N, P và Q theo thứ tự là trung điểm các cạnh AB, CD, BC và DA của tứ giác lồi ABCD
Khi đó :
\(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{BC}\right)\) và \(\overrightarrow{PQ}=\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{CD}\right)\)
Ta có : \(\left|\overrightarrow{MN}\right|+\left|\overrightarrow{PQ}\right|=\frac{1}{2}\left(\left|\overrightarrow{AD}+\overrightarrow{BC}\right|+\left|\overrightarrow{BA}+\overrightarrow{CD}\right|\right)\)
\(\le\frac{1}{2}\left(\left|\overrightarrow{AD}\right|+\left|\overrightarrow{BC}\right|+\left|\overrightarrow{BA}\right|+\left|\overrightarrow{CD}\right|\right)\)
Dấu đẳng thức xảy ra khi và chỉ khi \(\overrightarrow{AD}\uparrow\uparrow\overrightarrow{BC}\) và \(\overrightarrow{BA}\uparrow\uparrow\overrightarrow{CD}\)
Suy ra điều cần chứng minh

Tham khảo:
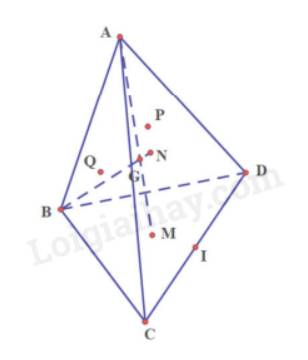
a) Ta có: M là trọng tâm của tam giác BCD
Nên M nằm trên trung tuyến BI (1)
Ta có: N là trọng tâm của tam giác ACD
Nên N nằm trên trung tuyến AI (2)
Từ (1) và (2) suy ra M và N thuộc mp (ABI)
b) Gọi H, K lần lượt là trung điểm của AG, BG
Ta có: HK // AB
AB // MN
Suy ra MN // HK
Theo định lý Ta-let, ta có: \(\frac{{GM}}{{GH}} = \frac{{GN}}{{GK}} = \frac{{MN}}{{HK}}(1)\)
Ta có:\(\frac{{HK}}{{AB}} = \frac{1}{2},\frac{{MN}}{{AB}} = \frac{1}{3}\)
Do đó \(\frac{{MN}}{{AB}}:\frac{{HK}}{{AB}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{HK}} = \frac{2}{3}(2)\)
Từ (1) và (2) suy ra\(\frac{{GM}}{{GH}} = \frac{2}{3}GH = \frac{1}{2}GA \Rightarrow \frac{{GM}}{{\frac{1}{2}GA}} = \frac{2}{3} \Rightarrow \frac{{GM}}{{GA}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GN}}{{GB}} = \frac{1}{3}\)
c) Gọi H, K lần lượt là trung điểm của BC, BD
Tam giác AHD có:\(\frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Suy ra: QM // AD
Do đó, tam giác QGM đồng dạng với tam giác DGA
Nên D, G, Q thẳng hàng
Ta có: QM // AD nên \(\frac{{QM}}{{AD}} = \frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Mà \(\frac{{QM}}{{AD}} = \frac{{QG}}{{GD}}\)
Do đó:\(\frac{{QG}}{{GD}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GP}}{{GC}} = \frac{1}{3}\)
Suy ra điều cần chứng minh.
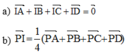

hôm trước thầy có ghi kết quả của trọng tâm tứ diện nên mình lấy kết quả đó để chứng minh luôn nhá
Gọi G là trọng tâm tứ diện. G chỉ được gọi là trọng tâm tứ diện <=> thỏa mãn 2 điều kiện sau:
1. \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\) ( hoàn toàn tương tự với vecto trọng tâm tác giác ta đã được học ở lớp 10 )
2. \(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}=4\overrightarrow{PG}\) ( với mọi P )
Gọi M và N lần lượt là trung điểm của AB và CD ( tự vẽ hình không khó đâu t vẽ ở olm thì nó mất time )
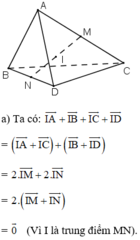
1. Ta có: \(\overrightarrow{GA}+\overrightarrow{GB}=2\overrightarrow{GM}\)
\(\overrightarrow{GC}+\overrightarrow{GD}=2\overrightarrow{GN}\)
Tương đương: \(2\left(\overrightarrow{GM}+\overrightarrow{GN}\right)=\overrightarrow{0}\) hay G là trung điểm của MN
Gọi H và K lần lượt là trung điểm của BC và AD
hoàn toàn chứng minh tương tự ta cũng có G là trung điểm của HK :)