Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(a\left(x-b\right)\left(x-c\right)+b\left(x-c\right)\left(x-a\right)+c\left(x-a\right)\left(x-b\right)=0\)
\(\Leftrightarrow a\left[x^2-x\left(b+c\right)+bc\right]+b\left[x^2-x\left(c+a\right)+ac\right]+c\left[x^2-x\left(a+b\right)+ab\right]=0\)
\(\Leftrightarrow x^2\left(a+b+c\right)-2x\left(ab+ac+bc\right)+3abc=0\) (1)
Xét với a + b + c \(\ne\) 0 thì phương trình (1) có biệt số \(\Delta'=\left(ab+bc+ac\right)^2-3.\left(a+b+c\right).abc\)
\(=a^2b^2+b^2c^2+c^2a^2+2abc\left(a+b+c\right)-3abc\left(a+b+c\right)\)
\(=a^2b^2+b^2c^2+c^2a^2-abc\left(a+b+c\right)\)
\(=\frac{a^2\left(b^2-2bc+c^2\right)+b^2\left(c^2-2ca+a^2\right)+c^2\left(a^2-2ab+b^2\right)}{2}\)
\(=\frac{a^2\left(b-c\right)^2+b^2\left(c-a\right)^2+c^2\left(a-b\right)^2}{2}\ge0\)
=> Phương trình (1) luôn có nghiệm trong trường hợp này.
Vậy phương trình ban đầu luôn có nghiệm với mọi a,b,c thỏa mãn \(a+b+c\ne0\)
Ta có : a (x−b)(x−c)+b(x−c)(x−a)+c(x−a)(x−b)=0
óa[x2−x(b+c)+bc]+b[x2−x(c+a)+ac]+c[x2−x(a+b)+ab]=0
óx2(a+b+c)−2x(ab+ac+bc)+3abc=0 (1)
Xét với a + b + c≠ 0 thì phương trình (1) có biệt số
Δ'=(ab+bc+ac)2−3.(a+b+c).abc
=a2b2+b2c2+c2a2+2abc(a+b+c)−3abc(a+b+c)=a2b2+b2c2+c2a2−abc(a+b+c)
=a2(b2−2bc+c2)+b2(c2−2ca+a2)+c2(a2−2ab+b2)2
a2(b−c)2+b2(c−a)2+c2(a−b)22 ≥0
=> Phương trình (1) luôn có nghiệm trong trường hợp này.
Vậy phương trình ban đầu luôn có nghiệm với mọi a,b,c thỏa mãn

a(x-b)(x-c)+b(x-a)(x-c)+c(x-a)(x-b)=0 (*)
<=> (a+b+c)x^2 -2x(ab+bc+ca) +3abc =0
D'(Delta ') = (ab+bc+ca)^2 - 3abc(a+b+c) (**)
Áp dụng BĐT vào (**): (x+y+z)^2/3 >= xy+yz+zx
<=> D' = (ab+bc+ca)^2 - 3abc(a+b+c) >= 0
=> Phương trình (*) luôn có nghiệm với mọi a, b, c
Ko chắc nha !
Minh Anh

Xin lựa a;b ... c;d e rỗng tuếch :>> (ko bt đúng ko nữa).
a, Thay m = 5 vào biểu thức ta đc
\(x^2-2\left(5+6\right)x+5-4=0\)
\(x^2-33x+1=0\)
\(\Delta=\left(-33\right)^2-4.1.1=1089-4=1085>0\)
Nên phương trình có 2 nghiệm phân biệt
\(x_1=\frac{33-\sqrt{1085}}{2};x_2=\frac{33+\sqrt{1085}}{2}\)
b, Ta có :
\(\Delta=\left(2m-2\right)^2-4\left(m-4\right)=4m^2-4-4m+16=4m^2-4m+12\)
\(=\left(4m^2-4m+1\right)+11\ge11\forall m\)
Vậy phuwong trình có 2 nghiệm phân biệt vs mọi x

a, Với x=2
PT<=> 4+2(m-2)-m+1=0
<=> m=-1
Vậy m=-1 thì phương trình có 1 nghiệm x=2
Ý sau dùng hệ thức Vi-et là ra

Câu 1:
Theo đề, ta có: \(x_1-x_2=1\)
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-2x_1x_2=m^2-2\cdot12=m^2-24\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1-x_2=m^2-24\\x_1-x_2=-m^2+24\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m^2-24=1\\-m^2+24=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m^2=25\\m^2=23\end{matrix}\right.\)
hay \(m\in\left\{5;-5;\sqrt{23};-\sqrt{23}\right\}\)

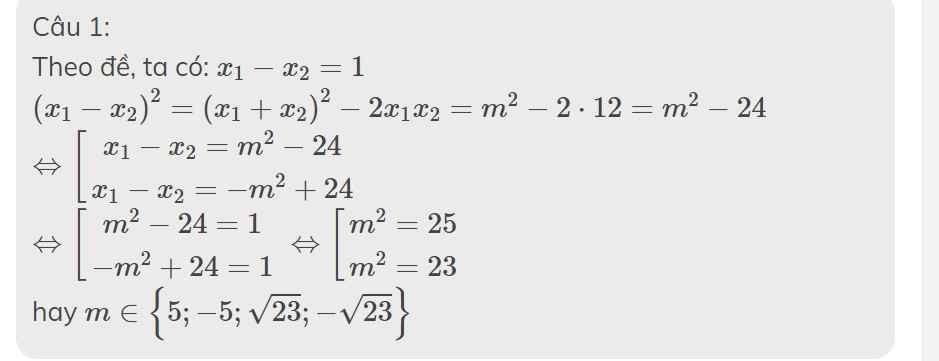
\(x\left(x-a\right)+x\left(x-b\right)+x\left(x-c\right)=0\)
\(x^2-ax+x^2-bx+x^2-cx=0\)
\(3x^2-\left(a+b+c\right)x=0\)
\(\Delta=\left(a+b+c\right)^2\ge0\forall a,b,c\)
=> phương trình luôn có nghiệm với mọi a,b,c