Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2:
Gọi tọa độ đỉnh D là D(x;y)
\(\overrightarrow{AB}=\left(-3;-2\right)\)
\(\overrightarrow{DC}=\left(1-x;1-y\right)\)
Vì ABCD là hình bình hành
nên \(\overrightarrow{AB}=\overrightarrow{DC}\)
=>\(\dfrac{-3}{1-x}=\dfrac{-2}{1-y}\)
\(\Leftrightarrow\dfrac{3}{x-1}=\dfrac{2}{y-1}\)
=>3y-3=2x-2
=>2x-2=3y-3
=>2x-3y=-1(1)
\(\overrightarrow{AD}=\left(x+1;y-6\right)\)
\(\overrightarrow{BC}=\left(5;-3\right)\)
Vì ABCD là hình bình hành nên \(\dfrac{x+1}{5}=\dfrac{y-6}{-3}\)
=>-3(x+1)=5(y-6)
=>-3x-3=5y-30
=>-3x-5y=-27
=>3x+5y=27(2)
Từ (1) và (2) suy ra x=4; y=3

a) Phương trình hoành độ giao điểm của (P) và (d) là:
\(\dfrac{x^2}{2}=mx-m+2\)
\(\Leftrightarrow\dfrac{1}{2}x^2-mx+m-2=0\)
\(\Delta=\left(-m\right)^2-4\cdot\dfrac{1}{2}\cdot\left(m-2\right)=m^2-2m+4>0\forall m\)
Do đó: (P) và (d) luôn cắt nhau tại hai điểm phân biệt(Đpcm)

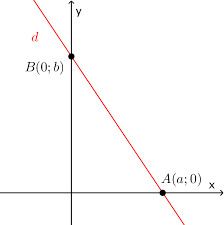
Gọi đường thẳng có dạng y = mx + n ( n khác 0 ) (1)
Vì đường thẳng cắt trục tung tại điểm b nên đt đi qua điểm có ( 0 ; b )
thay x = 0 ; y = b vào (1) ta có :
b = 0.m + n=> n = b
Vì đường thẳng cắt trục hoàng tại điểm có hoành độ là a nên dt đi qua điểm ( a; 0 )
thay x = a ; y = 0 ta có :
y = a.m + n <=> y = a.m + b => m = -b/a ( a khác 0 )
Đường thẳng đó có phương trính là \(y=\frac{-b}{a}.x+b\Leftrightarrow\frac{y}{b}=-\frac{x}{a}+1\Leftrightarrow\frac{x}{a}+\frac{y}{b}=1\)
Vậy ....

- xét phương trình hoành độ giao điểm : \(x^2=\left(2m-1\right)x-m+2\)\(\Leftrightarrow x^2-\left(2m-1\right)x+m-2=0\)có \(\Delta=\left(2m-1\right)^2-4\left(m-2\right)=4m^2-8m+9=\left(2m-1\right)^2+8\ge8\)vậy nên phương trinh luôn có 2 nghiệm phân biệt tức hai đồ thị luôn cắt nhau tại 2 điểm phân biệt A và B
- Có viet : \(\hept{\begin{cases}x_1+x_2=2m-1\\x_1x_2=m-2\end{cases}}\)ta có : \(A\left(x_1,y_1\right)=A\left(x_1,x_1^2\right)\)và \(B\left(x_2,y_2\right)=B\left(x_2,x_2^2\right)\)
nên ta có : \(x_1y_1+x_2y_2=0\Leftrightarrow x_1^3+x_2^3=0\)\(\Leftrightarrow\left(x_1+x_2\right)\left(\left(x_1+x_2\right)^2-3x_1x_2\right)=0\)\(\Leftrightarrow\left(2m-1\right)\left[\left(2m-1\right)^2-3m+6\right]=0\)
- \(2m-1=0\Leftrightarrow m=\frac{1}{2}\)
- \(\left(2m-1\right)^2-3m+6=0\Leftrightarrow4m^2-7m-7=0\)VN
2. Cho parabol (P): y = x2 và đường thẳng (d): y = 2(m – 1)x + m2 + 2m (m là tham số, m ∈ R )
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B?
b) Gọi H và K lần lượt là hình chiếu của A và B trên trục hoành.
Tìm m sao cho: OH2 + OK2 = 6 mọi người hướng dẫ mk ý b vs