Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài giải:
Khi mắc C1 và C2mắc nối tiếp thì: u = u1 + u2 = qC1+qC2qC1+qC2 vì q1 = q2 = q.
u=q(1C1+1C2)=qCu=q(1C1+1C2)=qC với 1C=1C1+1C21C=1C1+1C2
Suy ra: ZC =1Cω=1C1ω1C2ω1Cω=1C1ω1C2ω = ZC1+ZC2
cosωt (V) (ω và U không đổi) vào hai đầu đoạn mạch AB nối tiếp gồm điện trở R = 50 Ω, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C thay đổi được. Hình vẽ là đồ thị sự phụ thuộc điện áp hiệu dụng trên C vào biến số ωC. Công suất tiêu thụ của mạch khi ωC = 0,01 Ω
Bài này thì có vẹo gì đâu bạn.
\(u=100\sqrt 2\cos(100\pi t)(V)\)
\(Z_L=\omega L = 10\Omega\)
\(Z_C=\dfrac{1}{\omega C}=20\Omega\)
Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)
\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)
Suy ra: \(\varphi=\dfrac{\pi}{4}\)
Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)
ϕ1+ϕ2=90→tanϕ1.tanϕ2=1
→(ZL-ZC)2/R1.R2=1
→(ZL-ZC)=72→ZL=120
Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng
Công suất tiêu thụ của mạch gồm R và r là:
\(P=I^2\left(R+r\right)\)
\(2LC\omega^2=1\rightarrow2Z_L=Z_C\rightarrow2u_L=-uc\)
\(u_m=u_R+u_L+u_c=40+\left(-30\right)+60=70V\)
Chọn B
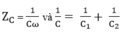
Gọi i = I0cosωt (A) là dòng điện qua mạch điện.
Vì C1 nối tiếp C2 nên u = u1 + u2; I1 = I2 = I,
Các điện áp hai đầu C1 và C2 đều chậm pha hơn i một góc π/2 và có giá trị hiệu dụng:
Nên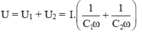
→ Tổng trở của mạch:
Vậy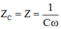
với 