Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Điểu chỉnh điện dung C của tụ thấy C = C1 và C = C2 thì có cùng giá trị hiệu dụng của tụ điện \(U_{C1} = U_{C2}\).
Khi đó để \(U_{Cmax}\) thì \(C=C_0 = \frac{C_1+C_2}{2}\)
Chọn đáp án.D.
Ta áp dụng điều kiện vuông pha với 2 đoạn mạch u1 và u2.
Khi đó: \(\tan\varphi_1.\tan\varphi_2=-1\)
\(\Leftrightarrow\frac{Z_L}{R}.\frac{Z_L-Z_C}{R}=-1\)
\(\Leftrightarrow R^2=Z_L\left(Z_C-Z_L\right)\)
Gọi i = I0cosωt (A) là dòng điện qua mạch điện.
Vì C1 nối tiếp C2 nên u = u1 + u2; I1 = I2 = I,
Các điện áp hai đầu C1 và C2 đều chậm pha hơn i một góc π/2 và có giá trị hiệu dụng:
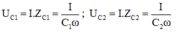
Nên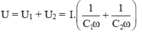 
→ Tổng trở của mạch:
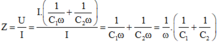
Vậy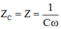 
với 
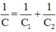
Công suất tiêu thụ của mạch gồm R và r là:
\(P=I^2\left(R+r\right)\)
R1 + R2 = U2/P => U=120 V
R1R2 =(ZL-ZC)2=5184
Cos$1 = R1/(R12+R1R2)0.5=0.6
Cos$2=R2/(R22+R1R2)0.5=0.8
Do \(L=rRC\) nên \(\dfrac{Z_L}{r}.\dfrac{-Z_C}{R}=-1\)
\(\Rightarrow \tan\varphi_{AM}. \tan\varphi_{MB}=-1\)
Suy ra đoạn mạch AM vuông pha với MB
\(\Rightarrow (\dfrac{u_{AM}}{U_{0AM}})^2+(\dfrac{u_{MB}}{U_{0MB}})^2=1\)
\(\Rightarrow (\dfrac{30}{U_{0AM}})^2+(\dfrac{40\sqrt 3}{U_{0MB}})^2=1\) (1)
Và: \(U_0^2=U_{0AM}^2+U_{0MB}^2=100^2\) (2)
Giải hệ (1) và (2)
Suy ra \(U_{0AM}=60V\); \(U_{0MB}=80V\)
AM MB AB 60 80 100 53 0 37 0
Từ hình vẽ ta thấy uMB sớm pha hơn uAB là \(37^0\approx \dfrac{\pi}{5} rad\)
Vậy: \(u_{MB}=80\cos(\omega t +\dfrac{\pi}{12}+\dfrac{\pi}{5})=80\cos(\omega t +\dfrac{17\pi}{60})(V)\)
Nhớ like và share nhé 
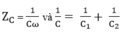
Bài giải:
Khi mắc C1 và C2mắc nối tiếp thì: u = u1 + u2 = qC1+qC2qC1+qC2 vì q1 = q2 = q.
u=q(1C1+1C2)=qCu=q(1C1+1C2)=qC với 1C=1C1+1C21C=1C1+1C2
Suy ra: ZC =1Cω=1C1ω1C2ω1Cω=1C1ω1C2ω = ZC1+ZC2