Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
\(\dfrac{a}{b}=\dfrac{a.\left(b+d\right)}{b.\left(b+d\right)}=\dfrac{ab+bd}{b^2+bd}\)
\(\dfrac{a+c}{b+d}=\dfrac{b\left(a+c\right)}{b\left(b+d\right)}=\dfrac{ab+bc}{b^2+bd}\)
Ta so sánh :
\(\dfrac{ab+bd}{b^2+bd}\) và \(\dfrac{ab+bc}{b^2+bd}\)
Vì cùng mẫu nên ta chỉ so sánh :
\(ab+bd\) và \(ab+bc\)
\(\Rightarrow\) Ta tiếp tục so sánh :
\(bd\) và bc thì ta có : bd < bc (1)
Từ 1, suy ra :
\(\dfrac{a}{b}< \dfrac{a+c}{b+c}\)
Mà \(\dfrac{a}{b}< \dfrac{c}{d}\)
Suy ra : \(\dfrac{a}{b}< \dfrac{a+c}{b+d}< \dfrac{c}{d}\) (đpcm)

3: Trường hợp 1: x<-3
Pt sẽ là -x-2-x-3=x
=>-2x-5=x
=>-3x=5
hay x=-5/3(loại)
Trường hợp 2: -3<=x<-2
Pt sẽ là -x-2+x+3=x
=>x=1(loại)
TRường hợp 3: x>=-2
Pt sẽ là x+2+x+3=x
=>2x+5=x
hay x=-5(loại)

Bài 1 : tham khảo trong đây nè!!
Câu hỏi của Hoàng Nguyễn Xuân Dương - Toán lớp 6 - Học toán với OnlineMath
Câu 1 :
a. Giả sử n2 + 2006 là số chính phương khi đó ta đặt n2 + 2006 = a2 ( a \(\in\) z ) \(\Leftrightarrow\) a2 - n2 = 2006 \(\Leftrightarrow\) ( a - n ) ( a + n ) = 2006 (*)
+ Thấy : Nếu a,n khác tính chất chẵn lẻ thì vế trái của (*) là số lẻ nên không thỏa mãn (*)
+ Nếu a,n cùng tính chất chẵn hoặc lẻ thì (a-n) chia hết 2 và (a+n) chia hết 2 nên vế trái chia hết cho 4 và vế phải không chia
hết cho 4 nên không thỏa mãn (*)
Vậy không tồn tại n để n2 + 2006 là số chính phương.
b. n là số nguyên tố > 3 nên không chia hết cho 3. Vậy n2 chia hết cho 3 dư 1 do đó n2 + 2006 = 3m + 1
+ 2006 = 3m+2007= 3(m+669) chia hết cho 3.
Vậy n2 + 2006 là hợp số.
Câu 2:Ta xét 3 trường hợp \(\dfrac{a}{\text{ }b}\) = 1 \(\dfrac{a}{b}\) > 1 \(\dfrac{a}{b}\) < 1
TH1: \(\dfrac{a}{b}\) =1 \(\Leftrightarrow a=b\) thì \(\dfrac{a+n}{b+n}\)thì\(\dfrac{a+n}{b+n}\) =\(\dfrac{a}{b}\) = 1
TH2: \(\dfrac{a}{b}>1\Leftrightarrow a+m>b+n\)
Mà \(\dfrac{a+n}{b+n}\) có phần thừa so với 1 là \(\dfrac{a-b}{b}\)vì \(\dfrac{a-b}{b+n}< \dfrac{a-b}{b}\) nên \(\dfrac{a+n}{b+n}< \dfrac{a}{b}\)
TH3: \(\dfrac{a}{b}< 1\Leftrightarrow a+n< b+n\)
Khi đó \(\dfrac{a+n}{b+n}\) có phần bù tới 1 là \(\dfrac{a-b}{b}\), \(\dfrac{a-b}{b}< \dfrac{b-a}{bb+n}\)
nên \(\dfrac{a+n}{b+n}>\dfrac{a}{b}\)
b. Cho A= \(\dfrac{10^{11}-1}{10^{12}-1}\) và A < 1 nên theo a, nếu \(\dfrac{a}{b}< 1\) thì \(\dfrac{a+n}{b+n}>\dfrac{a}{b}\Rightarrow A< \dfrac{\left(10^{11}-1\right)+11}{\left(10^{12}-1\right)+11}=\dfrac{10^{11}+10}{10^{12}+10}\)Do đó \(A< \dfrac{10^{11}+10}{10^{12}+10}=\dfrac{10\left(10^{10}+1\right)}{10\left(10^{12}+1\right)}\)Vậy A<B
Câu 3: Đặt B1 = a1
B2= a1+a2
B3= a1+a2+a3
còn lại làm tương tự như trên đến B10 = a1+a2+ ...+ a10
Nếu tồn tại Bi ( i= 1,2,3...10). nào đó chia hết cho 10 thì bài toán được chứng minh. ( 0,25 điểm).
Nếu không tồn tại Bi nào chia hết cho 10 ta làm như sau:
Ta đen Bi chia cho 10 sẽ được 10 số dư ( các số dư \(\in\) { 1,2.3...9}). Theo nguyên tắc Di-ric- lê, phải có ít nhất 2
số dư bằng nhau. Các số Bm -Bn, chia hết cho 10 ( m>n) \(\Rightarrow\) ĐPCM.


Ta có:
a1+a2+a3+...+an \(\equiv\) 0(mol 30)
=> a1+a2+a3+...+an chia hết cho 30
Ta lại có:
a1 \(⋮\)30 => a1.a1.a1.a1.a1 \(⋮\)30
a2 \(⋮\)30=> a2.a2.a2.a2.a2 \(⋮\)30
a3 \(⋮\)30=> a3.a3.a3.a3.a3 \(⋮\)30
.....
an \(⋮\)30=> an.an.an.an.an \(⋮\)30
Cộng vế với vế ta có:
ĐPCM
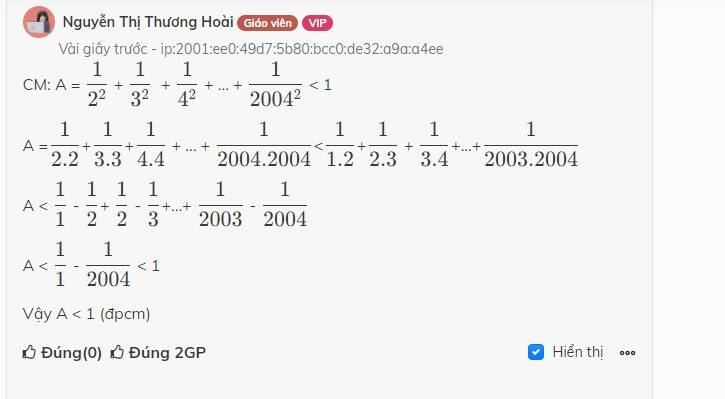
CM: A = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{4^2}\) + ... + \(\dfrac{1}{2004^2}\) < 1
A =\(\dfrac{1}{2.2}\)+\(\dfrac{1}{3.3}\)+\(\dfrac{1}{4.4}\) + ... + \(\dfrac{1}{2004.2004}\)<\(\dfrac{1}{1.2}\)+\(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\)+...+\(\dfrac{1}{2003.2004}\)
A < \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\)+ \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\)+...+ \(\dfrac{1}{2003}\) - \(\dfrac{1}{2004}\)
A < \(\dfrac{1}{1}\) - \(\dfrac{1}{2004}\) < 1
Vậy A < 1 (đpcm)