Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tại vì nó được đề bài cho nên có nghĩa,k có nghĩa thì lm kiểu đếch j?

Ta có:
\(5\left(x^3-9x\right)=5x^3-45x.\)(1)
\(\left(15-5x\right).\left(-x^2-3x\right)=-15x^2-45x+5x^3+15x^2=5x^3-45x\)(2)
Từ (1)(2) suy ra \(5\left(x^3-9x\right)=\left(15-5x\right)\left(-x-3x\right)\)
\(\Rightarrow\frac{x^3-9x}{15-5x}=\frac{-x^2-3x}{5}\)(Điều phải chứng minh)

\(a;x^2-3x+3=x^2-2\cdot\frac{3}{2}x+\frac{9}{4}-\frac{9}{4}+3\)
\(=\left(x-\frac{3}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\forall x\Leftrightarrow x^2-3x+3>0\forall x\)

câu 1
a)\(ĐKXĐ:x^3-8\ne0=>x\ne2\)
b)\(\frac{3x^2+6x+12}{x^3-8}=\frac{3\left(x^2-2x+4\right)}{\left(x-2\right)\left(x^2-2x+4\right)}=\frac{3}{x-2}\left(#\right)\)
Thay \(x=\frac{4001}{2000}\)zô \(\left(#\right)\)ta được
\(\frac{3}{\frac{4001}{2000}-2}=\frac{3}{\frac{4001}{2000}-\frac{4000}{2000}}=\frac{3}{\frac{1}{2000}}=6000\)

Bài 2: \(a,\frac{7x-1}{2x^2+6x}=\frac{7x-1}{2x\left(x+3\right)}=\frac{\left(7x-1\right)\left(x-3\right)}{2x\left(x+3\right)\left(x-3\right)}\)
\(\frac{5-3x}{x^2-9}=\frac{5-3x}{\left(x-3\right)\left(x+3\right)}=\frac{\left(5-3x\right)2x}{2x\left(x-3\right)\left(x+3\right)}\)
\(b,\frac{x+1}{x-x^2}=\frac{x+1}{x\left(1-x\right)}=-\frac{x+1}{x\left(x+1\right)}=-\frac{2\left(x-1\right)\left(x+1\right)}{2x\left(x-1\right)^2}\)
\(\frac{x+2}{2-4x+2x^2}=\frac{x+2}{2\left(x-1\right)^2}=\frac{2x\left(x+2\right)}{2x\left(x-1\right)^2}\)
\(c,\frac{4x^2-3x+5}{x^3-1}=\frac{4x^2-3x+5}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{2x}{x^2+x+1}=\frac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{6}{x-1}=\frac{6\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(d,\frac{7}{5x}=\frac{7.2\left(2y-x\right)\left(2y+x\right)}{2.5x\left(2y-x\right)\left(2y+x\right)}\)
\(\frac{4}{x-2y}=-\frac{4}{2y-x}=-\frac{4.2.5x\left(2x+x\right)}{2.5x\left(2y-x\right)\left(2y+x\right)}\)
\(\frac{x-y}{8y^2-2x^2}=\frac{x-y}{2\left(4y^2-x^2\right)}=\frac{x-y}{2\left(2y-x\right)\left(2y+x\right)}=\frac{5x\left(x-y\right)}{2.5x.\left(2y-x\right)\left(2y+x\right)}\)

Bài 1: (Sgk/36):
a. \(\dfrac{5y}{7}\)=\(\dfrac{20xy}{28x}\) vì
5y . 28x = 140xy
7 . 20xy = 140xy
=> 5y . 28x = 7 . 20xy
Vậy \(\dfrac{5y}{7}\)=\(\dfrac{20xy}{28x}\)
b. \(\dfrac{3x\left(x+5\right)}{2\left(x+5\right)}\)=\(\dfrac{3x}{2}\) vì
3x . 2(x+5) = 6x2+30x
2 . 3x(x+5) = 6x2+30x
=> 3x . 2(x+5) = 2 . 3x(x+5)
Vậy \(\dfrac{3x\left(x+5\right)}{2\left(x+5\right)}\)=\(\dfrac{3x}{2}\)
c. \(\dfrac{x+2}{x-1}\)=\(\dfrac{\left(x+2\right)\left(x+1\right)}{x^2-1}\) vì
(x+2) (x2-1) = (x+2) (x-1) (x-1)
=> (x+2) (x2-1) = (x-1) (x+2) (x+1)
Vậy \(\dfrac{x+2}{x-1}\)=\(\dfrac{\left(x+2\right)\left(x+1\right)}{x^2-1}\)
d. \(\dfrac{x^2-x-2}{x+1}\)=\(\dfrac{x^2-3x+2}{x-1}\)
(x-1) (x2-x-2) = x3-2x2-x+2
(x+1) (x2-3x+2) = x3-2x2-x+2
=> (x-1) (x2-x-2) = (x2-3x+2) (x+1)
Vậy \(\dfrac{x^2-x-2}{x+1}\)=\(\dfrac{x^2-3x+2}{x-1}\)

từ vế trái ta có
\(\frac{x.x\left(x+3\right)}{x.\left(x+3\right)\left(x+3\right)}\)
Rút gọn đi x và (x+3) còn
\(\frac{x}{x+3}\)
từ đó suy ra cái bên trên đó .
Xét VT, ta có: \(\frac{x^2\left(x+3\right)}{x\left(x+3\right)^2}=\frac{x}{x+3}\)= VP
Vậy ...
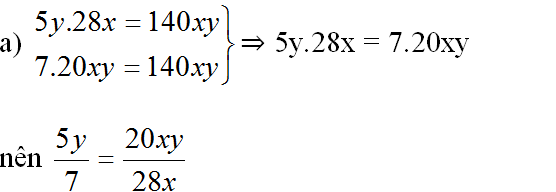
Để đẳng thức luôn có nghĩa thì (x - 1)2 + 2 \(\ne\) 0
mà (x - 1)2 + 2 > 0
=> đẳng thức luôn luôn có nghĩa