
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án:
Giải thích các bước giải:
Không tồn tại số a,b,c,d
Vì ta có abcd là số có 4 chữ số
abcd-d=7
Số có 4 chữ số - số đơn vị=7( vô lí)
=> không tồn tại a,b,c,d
học tốt

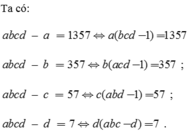
Nếu 1 trong a,b,c,d chẵn thì 1 trong 4 đẳng thức sai (kết quả ra chẵn do 1 số chẵn nhân 1 tích thì chẵn) =>a,b,c,d không tồn tại (do a,b,c,d phải thoả cả 4 đẳng thức)
Nếu a,b,c,d đều lẻ thì 1số lẻ nhân cho 1 số chẵn (tích 3 số lẻ trừ 1 thì chẵn) thì là một số chẵn=>a,b,c,d không tồn tại
Vậy không tồn tại các số nguyên a,b,c,d để thoả yêu cầu đề bài

Ta có:
abcd-a=2003
<=>a(bcd-1)=2003
<=>bcd-1=2003/a nguyên (vì bcd-1 nguyên)
suy ra a là ước của 2003
=>a lẻ
Tương tự ta có được b, c, d lẻ
Suy ra abcd lẻ
suy ra (abcd-a) ; (abcd-b)
(abcd-c) ; (abcd-d) đều chẵn
Mâu thuẫn với điều kiện
(2003 ; 2005 ; 2007 ; 2009 đều lẻ)
Vậy không tồn tại a,b,c,d thỏa mãn, thằng Quang ngu

abcd-a=2013
abcd-b=213
abcd-c=13
abcd-d=3
=>a,b,c,d cùng chẵn hoặc cùng lẻ
+) cùng lẻ=>abcd-a chẵn (vô lí)
cùng chẵn=>abcd-d chẵn (vô lí)
Vậy.......