Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong 1 tam giác, 3 đường phân giác cắt nhau tại 1 điểm và điểm đó cách đều 3 cạnh của tam giác (điểm này gọi là tâm đường tròn nộ tiếp). Nối E -> F; E -> D ; D -> F. Ta sẽ chứng minh H là giao điểm 3 đường phân giác.
Ta chứng minh được ∆AFC ~ ∆AEB(g.g) => AF/AE = AC/AB => AF/AC = AE/AB. => ta chứng minh được ∆AEF ~ ∆ABC(c.g.c) => góc AEF = góc ABC, chứng minh tương tư ta được ∆CED ~ ∆CBA => góc CED = góc ABC => góc AEF = góc CED ( = góc ABC), ta có: góc FEB = 90º - góc AEF và góc BED = 90º - góc CED, mà góc AEF = góc CED => góc FEB = góc BED => BE là phân giác góc FED => EH là phân giác góc FED, chứng minh tương tự ta được DH là phân giác góc EDF và FH là phân giác góc EFD
=> đpcm
bạn chứng minh rõ DH là tia phân giác cho mình đc k, k rõ cho lắm

a)cm tam giác AFC đồng dạng tam giác AEB(gg)
=> tam giác AFE đồng dạng ACB(cgc) . từ đó suy ra đpcm
b) tam giác BDH đồng dạng tam giác BEC (gg)
=> BH/BC =BD/BE hay BH .BE =BD.BC (1)
t^2 CH.CF=DC.BC (2)
lấy (1)+(2) theo vế suy ra đpcm
c)tam giác AFE đd tam giác ACB ( câu a) => góc AEF = góc C
t^2 tam giác DEC đd tam giác ABC => góc DEC= góc C
Do đó góc AEF= góc DEC
mà góc AEF+góc FEB=90 ; góc DEC+BED =90
=> góc FEB= góc BED
suy ra đpcm ................... (x-x)

a) Bạn hãy nhớ điều này: " 2 tam giác có đáy bằng nhau thì tỉ số diện tích = tỉ số 2 đường cao tương ứng 2 đáy, và 2 tam giác có 2 đường cao bằng nhau thì tỷ số diện tích = tỉ số 2 đáy tương ứng " - phần chứng minh xin nhường cho bạn vì nó không khó.
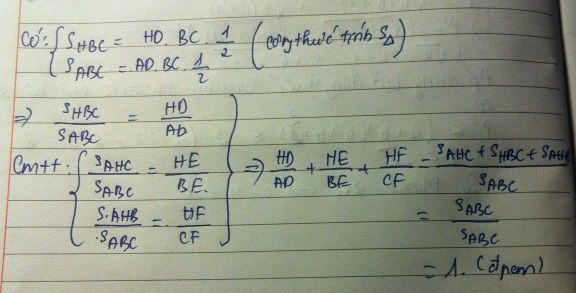
Áp dụng ta có: S(HDC)/S(ADC) = HD/AD (1). Chứng minh tương tự ta được S(BDH)/S(DAB) = HD/AD (2). Từ (1) và (2) => HD/AD = S(HDC)/S(ADC) = S(BDH)/S(DAB) = [ S(HDC) + S(BDH) ]/[ S(ADC) + S(DAB) ] = S(BHC)/S(ABC) (áp dụng tính chất dãy tỉ số bằng nhau)
=> HD/AD = S(BHC)/S(ABC) (3)
Chứng minh tương tự ta được:
HE/BE = S(AHC)/S(ABC) (4) và HF/CF = S(AHB)/S(ABC) (5)
Từ (3); (4) và (5) => HD/AD + HE/BE + HF/CF = S(BHC)/S(ABC) + S(AHC)/S(ABC) + S(AHB)/S(ABC) = [ S(BHC) + S(ACH) + S(ABH) ]/S(ABC) = S(ABC)/S(ABC) = 1
=> HD/AD + HE/BE + HF/CF = 1.
b) Ta chứng minh được ∆CHD ~ ∆CBF(g.g) - bạn tự chứng minh => CH/BC = CD/CF => CH.CF = BC.CD (6), chứng minh tương tự ta được: BH.BE = BC.DB (7). Từ (6) và (7) => BH.BE + CH.CF = BC.BD + BC.CD = BC(BD + CD) = BC²
c) Hãy nhớ lại kiến thức lớp 7: Trong 1 tam giác, 3 đường phân giác cắt nhau tại 1 điểm và điểm đó cách đều 3 cạnh của tam giác (điểm này gọi là tâm đường tròn nộ tiếp). Nối E -> F; E -> D ; D -> F. Ta sẽ chứng minh H là giao điểm 3 đường phân giác.
Ta chứng minh được ∆AFC ~ ∆AEB(g.g) => AF/AE = AC/AB => AF/AC = AE/AB. => ta chứng minh được ∆AEF ~ ∆ABC(c.g.c) => góc AEF = góc ABC, chứng minh tương tư ta được ∆CED ~ ∆CBA => góc CED = góc ABC => góc AEF = góc CED ( = góc ABC), ta có: góc FEB = 90º - góc AEF và góc BED = 90º - góc CED, mà góc AEF = góc CED => góc FEB = góc BED => BE là phân giác góc FED => EH là phân giác góc FED, chứng minh tương tự ta được DH là phân giác góc EDF và FH là phân giác góc EFD
=> đpcm
mình copy cho bạn lời giải đó
Xét tứ giác BFHD có \(\widehat{BFH}+\widehat{BDH}=90^0+90^0=180^0\)
nên BFHD là tứ giác nội tiếp
Xét tứ giác CEHD có \(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)
nên CEHD là tứ giác nội tiếp
Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp
Ta có: \(\widehat{FDH}=\widehat{FBH}\)(BFHD nội tiếp)
\(\widehat{EDH}=\widehat{ECH}\)(EHDC nội tiếp)
mà \(\widehat{FBH}=\widehat{ECH}\left(=90^0-\widehat{BAC}\right)\)
nên \(\widehat{FDH}=\widehat{EDH}\)
=>DH là phân giác của góc FDE
Ta có: \(\widehat{EFH}=\widehat{EAH}\)(AEHF nội tiếp)
\(\widehat{DFH}=\widehat{DBH}\)(BFHD nội tiếp)
mà \(\widehat{EAH}=\widehat{DBH}\left(=90^0-\widehat{ACD}\right)\)
nên \(\widehat{EFH}=\widehat{DFH}\)
=>FH là phân giác của góc EFD
Xét ΔEFD có
DH,FH là các đường phân giác
DH cắt FH tại H
Do đó: H là tâm đường tròn nội tiếp của ΔEFD
hay H cách đều ba cạnh của ΔEFD