Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C A' C' B' H a b c
\(AA'=c.sinB=b.sinC\Leftrightarrow\frac{c}{sinC}=\frac{b}{sinB}.\)
va\(BB'=c.sinA=a.sinC\Leftrightarrow\frac{c}{sinC}=\frac{a}{sinA}\)
\(\Leftrightarrow\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}\)
\(S_{\Delta ABC}=\frac{1}{2}.a.AA'=\frac{1}{2}.a.bsinC\)

Tham khảo:

Chứng minh định lý hàm cos
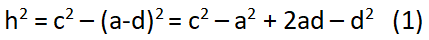
Chứng minh định lý hàm cos – Phương trình 1
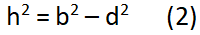
Chứng minh định lý hàm cos – Phương trình 2

Chứng minh định lý hàm cos – Phương trình 3
Với d = b cosC thế vào phương trình biến đổi (3) ta rút ra điều phải chứng minh!

A B C E D H K
a/ Áp dụng định lý Pytago:
\(\frac{AC^2+CB^2-BA^2}{CB^2+BA^2-AC}=\frac{AK^2+KC^2+\left(BK^2++CK^2\right)-AB^2}{\left(BK+CK\right)^2+BA^2-\left(AK+KC\right)^2}\)
\(=\frac{2CK^2+2BK.CK}{2BK^2+2BK.CK}=\frac{2CK\left(CK+BK\right)}{2BK\left(BK+CK\right)}=\frac{CK}{BK}\)
b ) Ta có :
\(\tan B=\frac{AK}{BK}\) ; \(\tan C=\frac{AK}{CK}\)
Nên \(\tan B.\tan C=\frac{AK^2}{BK.CK}\left(1\right)\)
Mặt khác ta có : \(B=HKC\)mà : \(tanHKC=\frac{KC}{KH}\)
Nên \(\tan B=\frac{KC}{KH}\)tương tự \(tanC=\frac{KB}{KH}\)
\(\Rightarrow\tan B.\tan C=\frac{KB.KC}{KH^2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left(\tan B.\tan C\right)^2=\left(\frac{AK}{KH}\right)^2\)
Theo bài ra có : \(HK=\frac{1}{3}AK\Rightarrow\tan B.\tan C=3\)
c ) c/ Ta chứng minh được: 2 tam giác ABC và ADE đồng dạng nên :
\(\frac{S_{ABC}}{S_{ADE}}=\left(\frac{AB}{AD}\right)^2\left(3\right)\)
Mà góc BAC = 60 0 nên \(\widehat{ABD}=30^0\)
\(\Rightarrow AB=2AD\left(4\right)\)
Từ (3) và (4 ) ta có : \(\frac{S_{ABC}}{S_{ADE}}=4\Rightarrow S_{ADE}=30\left(cm^2\right)\)
Chúc bạn học tốt !!!

C A B H
Gọi AH là đường cao của tam giác ABC như hình vẽ
ta có : \(AH=AC\times sinC=b.sinC\)
mà \(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}AC.BC.sinC=\frac{1}{2}ab.sinC\)
.b hoàn toàn tương tự ta có thể chứng minh :
\(S_{ABC}=\frac{1}{2}ab.sinC=\frac{1}{2}bc.sinA=\frac{1}{2}ac.sinB\)
hay \(abc.\frac{sinC}{c}=abc.\frac{sinA}{a}=abc.\frac{sinB}{b}\)
hay ta có : \(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}\)

A B C D E a b c
a) Kẻ \(CE\perp AB\)
Ta có : \(S_{\Delta ABC}=\frac{1}{2}CE.AB\left(1\right)\)
Xét \(\Delta ACE\)có \(\sin A=\frac{EC}{AC}\)
\(\Rightarrow\frac{1}{2}AB.AC.\sin A=\frac{1}{2}AB.AC.\frac{EC}{AC}=\frac{1}{2}AB.EC\left(2\right)\)
Từ (1) và (2) \(\Rightarrow S_{\Delta ABC}=\frac{1}{2}AB.AC.\sin A\left(đpcm\right)\)
b) Kẻ \(BD\perp AC\)
Xét \(\Delta ADB\)có \(\sin A=\frac{BD}{AB}\)
\(\Rightarrow\frac{a}{\sin A}=BC\div\frac{BD}{AB}=\frac{BC.AB}{BD}\left(3\right)\)
Lại có : \(\sin A=\frac{EC}{AC}\)( câu a )
\(\Rightarrow\frac{a}{\sin A}=BC\div\frac{EC}{AC}=\frac{CA.BC}{EC}\left(4\right)\)
Xét \(\Delta BEC\)có \(\sin B=\frac{EC}{BC}\)
\(\Rightarrow\frac{b}{\sin B}=CA\div\frac{EC}{BC}=\frac{CA.BC}{EC}\left(5\right)\)
Xét \(\Delta BDC\)có \(\sin C=\frac{DB}{BC}\)
\(\Rightarrow\frac{c}{\sin C}=AB\div\frac{DB}{BC}=\frac{AB.BC}{DB}\left(6\right)\)
Từ (3) ; (4) ; (5) và (6) \(\Rightarrow\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\left(đpcm\right)\)
c) Xét \(\Delta ABD\)có \(\cos A=\frac{AD}{AB}\)
Áp dụng định lí Py-ta-go cho \(\Delta ABD\)vuông tại D ta được :
\(AB^2=BD^2+AD^2\)
Áp dụng định lí Py-ta-go cho \(\Delta BDC\)vuông tại D ta được :
\(BD^2+DC^2=BC^2\)
Ta có : \(b^2+c^2-2bc.\cos A\)
\(=AB^2+AC^2-2AB.AC.\cos A\)
\(=BD^2+AD^2+AC^2-2AB.AC.\frac{AD}{AB}\)
\(=BD^2+\left(AC^2-2AD.AC+AD^2\right)\)
\(=BD^2+\left(AC-AD\right)^2\)
\(=BD^2+DC^2\)
\(=BC^2=a\left(đpcm\right)\)
ai giải dùm mik xem cái, nhớ vẽ hình