
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi \(d\inƯ\left(n+15;n+72\right)\) ( \(d\in N,d\ne0\))
\(\Rightarrow n+15⋮d\)
\(n+72⋮d\)
\(\Rightarrow\left(n+72\right)-\left(n+15\right)⋮d\)
\(\Rightarrow57⋮d\)
\(\Rightarrow d=1;3;19;57\) để n + 15 và n + 72 là hai số nguyên tố cùng nhau thì n khác dạng 19k + 15
Vậy có vô số giá trị n

Chiều dài căn phòng sau khi tăng là:
7+2/7.7=9(m)
Chiều rộng căn phòng ban đầu là:
45/9=5(m)
Tỉ số giữa chiều dài và chiều rộng ban đầu của căn phòng là:
7/5=1,4
Vậy............................................................
Chúc bạn học tốt ! ![]()
sao phải nhân 7 ở lời giải thứ nhát z bạn Trần Minh Hưng

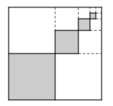
Gọi diện tích các hình vuông được tô lần 1,2,3,...,n,... lần lượt là ![]()
Khi đó diện ta tính được 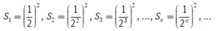
Vậy tối thiểu An phải tô đến hình vuông thứ 5 thì diện tích của hình vuông được tô nhỏ hơn 1 1000
Chọn C.

Đáp án C
Chọn đáp án C vì dãy ở đây là một CSN có công bội q = 3 2 > 1 , nên dãy 3 2 , 9 4 , 27 8 , . . . , 3 2 n không phải là dãy lùi vô hạn

Đáp án D.
Cách 1: Tư duy tự luận
z = − 25 = 25. − 1 = 25 i 2 → z 1,2 = ± 5 i
Cách 2: Sử dụng máy tính cầm tay

Vậy các căn bậc hai của số phức z là z 1,2 = ± 5 i

Đáp án C
Phương pháp:
Phương trình bậc nhất đối với sin và cosasinx + bcosx = c vô nghiệm ![]()
Cách giải: Phương trình sinx + (m+1)cosx = 2 vô nghiệm
![]()
![]()
Gỉa sử \(\sqrt{15}\) là số hữu tỉ
=> \(\sqrt{15}=\frac{m}{n}\)( trong đó \(\frac{m}{n}\) là phân số tối giản)=> \(15=\frac{m^2}{n^2}\) hay \(15n^2=m^2\)(1)
Từ (1) => \(m^2\) chia hết cho 15 => m chia hết 15
Đặt m=15k( \(k\in Z\))=> \(m^2=225k^2\)(2)
Tứ (1);(2)=> \(15n^2=225k^2\)=> \(n^2=15k^2\)(3)
Từ (3) => \(n^2\)chia hết cho 15 => n chia hết cho 15
=> \(\frac{m}{n}\)không phải là phân số tối giản trái với giả thiết => \(\sqrt{15}\)không phải là số hửu tỉ
Vậy \(\sqrt{15}\)là số vô tỉ(dpcm)
Giả sử \(\sqrt{7}\) là số hữu tỉ, như vậy có thể viết dưới dạng phân số tối giản \({m\over n}\) tức là \(\sqrt{7} = {m \over n}\) . Suy ra \(7={m^2 \over n^2}\) hay \(7m^2=n^2\) (1)
Đảng thức (1) chứng tỏ \(m^2\vdots7\) mà 7 là số nguyên tố nên \(m\vdots7\) .
Đặt\(m=7k\) (k∈ℤ) ta có \(m^2=49k^2\) (2)
Từ (1) và (2) suy ra \(7n^2=49k^2\) nên \(n^2=7k^2\) (3)
Từ (3) ta lại có \(n^2\vdots7\) và vì 7 là số nguyên tố nên \(n\vdots7\) .
Như vậy m và n cùng chia hết cho 7 nên phân số \({m \over n}\) không tối giản, trái với giả thiết. Vậy \(\sqrt{7}\) không phải là số hữu tỉ, do đó \(\sqrt7\) là số vô tỉ