K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 10 2018
b) \(\dfrac{\sqrt{a}}{\sqrt{a}-\sqrt{b}}-\dfrac{\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\dfrac{2b}{a-b}\)
\(=\dfrac{\sqrt{a}}{\sqrt{a}-\sqrt{b}}-\dfrac{\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\dfrac{2b}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)-\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)-2b}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{a+\sqrt{ab}-\sqrt{ab}+b-\sqrt{ab}+b-2b}{a-b}\)
\(=\dfrac{a}{a-b}\)
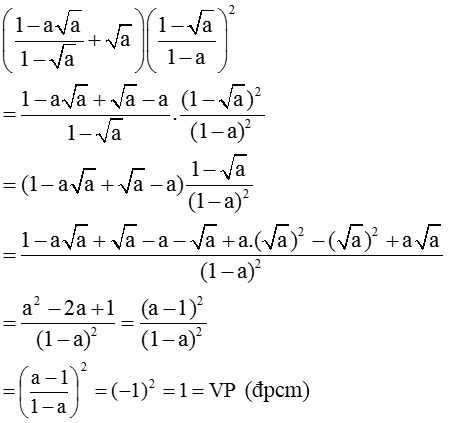
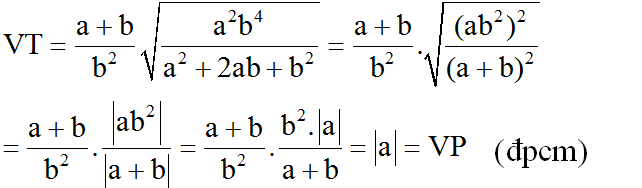
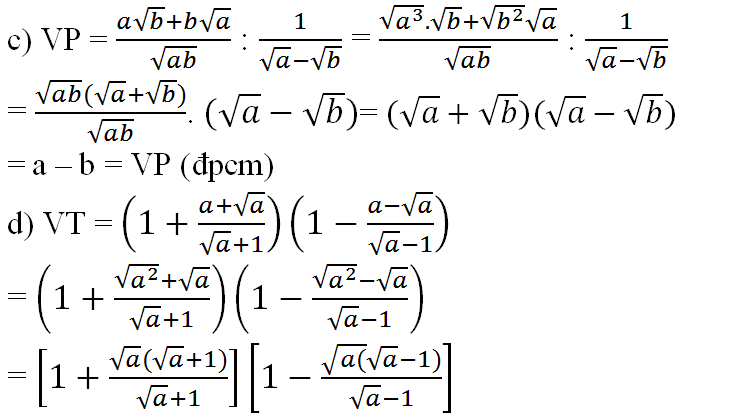
a) \(\dfrac{a^6+b^6}{2}\ge3a^2b^2-4\)
\(\Leftrightarrow a^6+b^6\ge6a^2b^2-8\)
\(\Leftrightarrow a^6+b^6+8\ge6a^2b^2\)
Áp dụng BĐT Cauchy, ta có:
\(a^6+b^6+8\ge3\sqrt[3]{a^6.b^6.8}=6a^2b^2\)
Vậy ta có đpcm
b) Tương tự
mình cũng vừa ra xong nhưng cũng cảm ơn bạn