LL
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
22 tháng 9 2020
1.
AB=CD (cặp cạnh đối hbh)
AM=AB/2 và CN=CD/2
=> AM=CN (1)
AM thuộc AB; CN thuộc CD mà AB//CD => AM//CN (2)
Từ (1) và (2) => AMCN là hbh(Tứ giác có một cặp cạnh đối // và = nhau thì tứ giác đó là hbh)
2.
a. M là trung điểm AB; N là trung điểm AC => MN là đường trung bình của tgABC
=> MN//BC => MN//BP và MN=BP=BC/2
=> BMNP là hbh (lý do như bài 1)
b. Ta có BMNP là hbh và ^B=90 => BMNP là HCN
\(BC=\sqrt{AC^2-AB^2}=\sqrt{5^2-3^2}=4cm.\)
Từ kq câu a => MN=BC/2=4/2=2 cm
C/m tương tự câu a có NP là đường trung bình của tg ABC => NP=AB/2=3/2=1,5 cm
Chu vi BMNP là
(2+1,5)x2=7 cm
6 tháng 11 2021
b: Xét tứ giác ADME có
AD//ME
AE//DM
Do đó: ADME là hình bình hành
FG
7 tháng 11 2017
mình rảnh nên mình vẽ thôi :V A B C D M E
a. xét tam giác ABC, có:
M là trung điểm AB (giả thuyết)
D là trung điểm BC (AD là đường trung tuyến tam giác ABC)
=> MD là đường trung bình tam giác ABC
=> MD // AC
mà E thuộc MD (E là điểm đối xứng của D qua M)
=> DE // AC (1)
ta có: MD là đường trung bình tam giác ABC (chứng minh trên)
=> MD = \(\frac{1}{2}\)AC
mà M là trung điểm cua ED (E là điểm đối xứng của D qua M)
=> ED = AC (2)
từ (1),(2):
=> AEDC là hình bình hành (tứ giác có 1 cặp cạnh đối vừa song song, vừa bằng nhau) (chỗ này đề sai nên mình sửa lại là AEDC)
b. xét tứ giác AEBD, có:
M là trung điểm ED (E là điểm đối xúng của D qua M)
M là trung điểm AB (giả thuyết)
ED cắt AB tại M
=> AEBD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)
xét tam giác ABC vuông A, có:
AD là đường trung tuyến (giả thuyết)
=> AD = BD
mà AEBD là hình bình hành (chứng minh trên)
=> AEBD là hình thoi (hình bình hành có 2 cặp cạnh kề bằng nhau)
C. ta có: D là trung điểm của BC (AD là đường trung tuyến)
=> BD = \(\frac{1}{2}\)BC
=> BD= \(\frac{5}{2}\)
=> BD= 2.5 cm
ta có: AEBD là hình thoi (chứng minh trên)
=> P(chu vi)AEBD = 2.5x4
= 10 cm
CM
26 tháng 5 2017
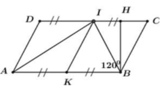
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD
=> SABCD = BH.CD
Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.
=> 2(AB + BC) = 60 ó 2.3BC = 60 ó BC = 10cm
Xét tứ giác KICB ta có:
IC = BC = KB = IK = 1 2 AB = 10cm
=> IKBC là hình thoi (dấu hiệu nhận biết).
Mà B ^ = 1200 => I C B ^ = 1800 – 1200 = 600
Xét tam giác ICB có: I C = B C I C B = 60 0
=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 600).
=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.
=> HI = HC = 1 2 BC = 5cm
Áp dụng định lý Pytago với tam giác vuông HBC ta có:
BH = B C 2 − H C 2 = 10 2 − 5 2 = 75 = 5 3 cm
=> SABCD = BH.AB = BH.2BC = 5 3 .2.10 = 100 3 cm2
Đáp án cần chọn là: A