Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TGọi độ dài cạnh bên là b. Ta có b=(15-a)/2
Do b\(\in\)N => a là số lẻ => a\(\in\)\(\left\{1;3;5;7;9;11;13\right\}\).
Vậy a\(\in\)\(\left\{1;3;5;7;9;11;13\right\}\)

Đáp án D.
Gọi thiết diện qua trục là tam giác cân SAB có S A = 2 A B .
Ta có:
S O 2 = S A 2 − A O 2 = 4 A B 2 − O A 2 = 15 r 2 = h 2 ⇒ r = 15 5 c m .
Diện tích xung quanh của hình nón là: S x q = π r l = π r h 2 + r 2 = 12 5 c m 2 .

Xin lỗi mình thiếu:
Theo mình thì giải như sau: Gọi độ dài hai cạnh góc vuông là a và b với a>b>0
2 cạnh góc vuông có độ dài hơn kém nhau 4cm ta có a-b=4
suy ra a = b+4.
Theo Pitago ta có a^2+b^2=20^2. Thay a=b+4 ta có:
(b+4)^2 + b^2 = 400
<=> b^2 + 4b - 192 = 0
<=> b^2 -12b + 16b - 192 = 0
<=> b(b-12)+16(b-12)=0
<=> (b-12)(b+16)=0
suy ra b -12=0 hoặc b+16=0
vậy b=12 (thỏa mãn) hoặc b = -16 (loại vì b>0)
Với b = 12 thì a = 12+4=16.
Vậy chu vi của hình tam giác là: dễ rồi tự làm
UfO S đừng nói như vậy, đây cũng là một bài khó đấy với trình độ của lớp 8.
Chưa chắc bạn đã làm nổi đâu Ufo S ạ.
Theo mình thì giải như sau: Gọi độ dài hai cạnh góc vuông là a và b với a>b>0
2 cạnh góc vuông có độ dài hơn kém nhau 4cm ta có a-b=4
suy ra a = b+4.
Theo Pitago ta có a^2+b^2=20^2. Thay a=b+4 ta có:
(b+4)^2 + b^2 = 400
<=> b^2 + 4b - 192 = 0
<=> b^2 -12b + 16b - 192 = 0
<=> b(b-12)+16(b-12)=0
<=> (b-12)(b+16)=0
suy ra b -12=0 hoặc b+16=0
vậy b=12 (thỏa mãn) hoặc b = -16 (loại vì b>0)
Với b = 12 thì a = 12+4=16.
Vậy độ dài hai cạnh góc vuông là 12cm và 16cm.

Ta có: S A ⊥ A B ; S A ⊥ A C ; B C ⊥ A B ; B C ⊥ S A
Suy ra, B C ⊥ S A B nên: B C ⊥ S B
Do đó, tứ diện S.ABC có 4 mặt đều là các tam giác vuông.
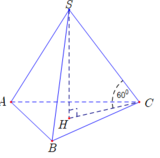
Ta có: AB là hình chiếu của SB lên (ABC) nên S B A ^ = 60 o
tan S B A ^ = S A A B ⇒ A B = S A tan S B O ^ = a 3 3 = a = B C A C = A B 2 + B C 2 = a 2 + a 2 = a 2 S B = S A 2 + A B 2 = a 3 3 + a 2 = 2 a
Do đó ta có
S t p = S S A B + S S B C + S S A C + S A B C = 1 2 S A . A B + S B . B C + S A . A C + A B . B C = 1 2 a 3 . a + 2 a . a + a 3 . a 2 + a . a = 3 + 3 + 6 2 a 2
Vậy S t p = 3 + 3 + 6 2 a 2
Đáp án A

Đáp án là B
Ta có:
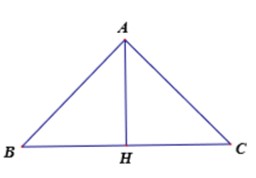
• S A B C = 6 2 3 4 = 9 3 c m 2 ; S H = S A . sin 60 0 = 3 3 2 ( c m )
• S S A B = 1 3 .9 3 . 3 3 2 = 27 2 c m 3

(Diện tích hình thang là 3,75cm2 và chiều cao là 10cm thì không cân đối. Chỉnh lại diện tích là 375cm2 )
Hai tam giác KCD và KAC có chung đường cao kẻ từ C nên hai cạnh đáy KD và KA có tỉ lệ 1.5/1 = 3/2 hay KA = AD x 2
Và trong hình thang ABCD có SADC = SBDC
Nên ta được:
SBDC = SDAC = 1/2SKAC ﴾1﴿
=> KB =BC x 2 => BC = 1/3 KC SABC = 1/3KAC ﴾2﴿
Từ ﴾1﴿ và ﴾2﴿ ta được :
SABC/SDAC = 2/3
Hai tam giác ABC và ADC có hai cạnh đáy là AB và CD và hai đường cao tương ứng bằng nhau ﴾bằng đường cao hình thang﴿ nên hai cạnh đáy sẽ tỉ lệ với hai diện tích.
AB/CD = 2/3
Tổng hai cạnh đáy AB và CD là : 375 x 2 : 10 = 75 ﴾cm﴿
Tổng số phần bằng nhau 3 + 2 = 5 ﴾phần﴿
Đáy ngắn AB là : 75 : 5 x 2 = 30 ﴾cm﴿
Đáy CD là: 75 – 30 = 45 ﴾cm﴿



Nếu đó là cạnh đáy thì bài toán được chứng minh.
Nếu đó là cạnh bên theo bất đẳng thức tam giác ta có 4x2=8<13(vô lí).
Vậy đó là cạnh đáy.
do tam giác cân nên ta có độ dài 3 cạnh tam giác là: a, a, b
theo đề ta có: 2a+ b= 21
giả sử cạnh đó là cạnh bên---> 2.4+ b= 21<---> b= 21- 8=13---> 2a< b
mà ta lại có: trong 1 tam giác tổng của 2 cạnh luôn luôn lớn hơn cạnh còn lại
----> điều giả sử là vô lý---> cạnh đó là cạnh đáy.