Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D S E K H
Gọi H là trung điểm của AB, suy ra \(SH\perp\left(ACBD\right)\)
Do đó \(SH\perp HD\) ta có :
\(SH=\sqrt{SD^2-DH^2}=\sqrt{SD^2-\left(AH^2+AD^2\right)}=a\)
Suy ra \(V_{s.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{a^2}{3}\)
Gọi K là hình chiếu vuông góc của H trên BD và E là hình chiếu vuông góc của H lên SK. Ta có :
\(\begin{cases}BD\perp HK\\BD\perp SH\end{cases}\) \(\Rightarrow BH\perp\) (SHK)
=> \(BD\perp HE\) mà \(HE\perp SK\) \(\Rightarrow HE\perp\) (SBD)
Ta có : HK=HB.\(\sin\widehat{KBH}\)\(=\frac{a\sqrt{2}}{4}\)
Suy ra \(HE=\frac{HS.HK}{\sqrt{HS^2+HK^2}}=\frac{a}{3}\)
Do đó \(d\left(A:\left(SBD\right)\right)\)=2d(H; (SBD)) =3HE=\(\frac{2a}{3}\)

Khá là dài, mình tìm ra được bằng \(\dfrac{3\sqrt3}{64}a^3\)

gọi H là hình chiếu vuông góc của S lên (ABCD) khi đó SH vuông góc với AB.khi đó dung SH song song với Az và chọn gốc tọa độ tại A

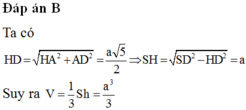


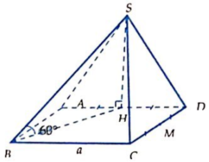
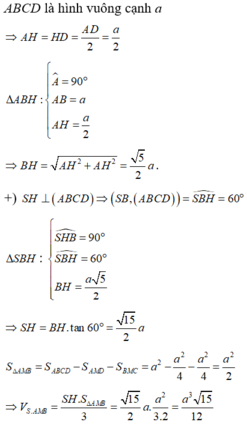
Do H là trung điểm của AB,
=> SH vuông (ABCD)
Do đó SH vuông HD. Có \(SH=\sqrt{SD^2-DH^2}=\sqrt{SD^2-\left(AH^2+AD^2\right)}=a\)
\(\Rightarrow V_{S.ABCD}=\frac{1}{3}S.H.S_{ABCD}=\frac{a^3}{3}\)
Gọi K là hình chiếu vuông góc với H trên BD vs2 E là là hình chiếu vuông góc của H trên SK.
Có : BD vuông HK, BD vuông SH, BD vuông (SHK)
=> BD vuông HE.
Mà HE vuông SK
Do đó HE vuông (SBD)
Ta có : HK = HB \(\sin\widehat{KBH}=\frac{a\sqrt{2}}{4}\)
=> HE = \(\frac{HS.HK}{\sqrt{HS^2+HK^2}}=\frac{4}{3}\)
Do đó, d (A,(SBD)) = 2d (H,(SBD)) = 2HE = 2a/3