Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do đề ko thấy yêu cầu gì là 2 số phân biệt nên làm theo hướng đó.
Không gian mẫu: \(12^2=144\)
Chọn số nguyên tố chẵn: có đúng 1 cách là chọn số 2
Chọn số nguyên tố lẻ nhỏ hơn 13: có 4 cách (3,5,7,11)
\(\Rightarrow2.4.2!=16\) cách
Xác suất: \(P=\dfrac{16}{144}=...\)

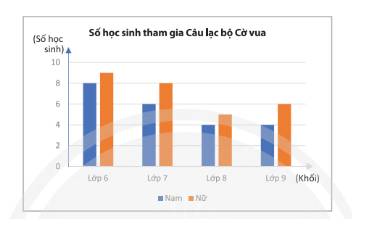
Tổng số học sinh tham gia câu lạc bộ là:
\(8 + 9 + 6 + 8 + 4 + 5 + 4 + 6 = 50\) (học sinh)
- Biến cố \(A\) xảy ra khi bạn học sinh chọn được là nữ.
Số học sinh nữ tham gia câu lạc bộ là:
\(9 + 8 + 5 + 6 = 28\) (học sinh)
Xác suất của biến có \(A\) là:
\(P\left( A \right) = \frac{{28}}{{50}} = \frac{{14}}{{25}}\)
- Biến cố \(B\) xảy ra khi bạn học sinh chọn được là học sinh lớp 8.
Số học sinh lớp 8 trong câu lạc bộ là:
\(4 + 5 = 9\)(học sinh)
Xác suất của biến có \(B\) là:
\(P\left( B \right) = \frac{9}{{50}}\)
- Biến cố \(C\) xảy ra khi bạn học sinh chọn được là nam và không học lớp 7.
Số học sinh câu lạc bộ là nam và không học lớp 7 là:
\(8 + 6 + 4 = 18\)
Xác suất của biến có \(C\) là:
\(P\left( C \right) = \frac{{18}}{{50}} = \frac{9}{{25}}\)

a: Số cách viết ngẫu nhiên một số tự nhiên có 2 chữ số là:
99-10+1=90(số)
b: Số số chẵn có 2 chữ số là: \(\dfrac{98-10}{2}+1=\dfrac{88}{2}+1=45\left(số\right)\)
=>Xác suất viết được một số chẵn là \(\dfrac{45}{90}=\dfrac{1}{2}\)
Số số tròn chục có 2 chữ số là: \(\dfrac{90-10}{10}+1=9\left(số\right)\)
=>Xác suất viết ra được một số tròn chục là \(\dfrac{9}{90}=\dfrac{1}{10}\)
Các số có 2 chữ số mà là bình phương của một số tự nhiên là 16;25;36;49;64;81
=>Có 6 số
=>Xác suất viết được là 6/90=1/15

Gọi \(A\) là biến cố người được chọn ngẫu nhiên ủng hộ việc tắt điện trong sự kiện Giờ Trái Đất.
Xác suất thực nghiệm của biến cố \(A\) là \(\frac{{255}}{{300}} = 0,85\).
Do số người chọn lớn nên \(P\left( A \right) \approx 0,85\).
Vậy xác suất của biến cố “Một người được lựa chọn ngẫu nhiên trong khu dân cư ủng hộ việc tắt đèn điện trong sự kiện Giờ Trái Đất” khoảng 0,85.

- Các tấm thẻ được đánh số chẵn là: thẻ số 2; thẻ số 8; thẻ số 32.
Xác suất để biến cố \(A\) xảy ra là \(\frac{3}{6} = \frac{1}{2}\)
- Các tấm thẻ được đánh số nguyên tố là: thẻ số 2; thẻ số 3; thẻ số 5; thể số 13.
Xác suất để biến cố \(B\) xảy ra là \(\frac{4}{6} = \frac{2}{3}\)
- Không có tấm thẻ nào được đánh số chính phương.
Do đó, xác suất để biến cố \(C\) xảy ra bằng 0.

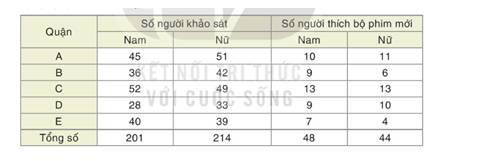
a) Có tổng 101 người ở quận C tham gia khảo sát => Có 101 kết quả có thể của hành động trên
Có 26 người thích bộ phim đó => Có 26 kết quả thuận lợi cho biến cố A . Vậy \(P(A) = \frac{{26}}{{101}} \approx 0,257\)
b) Có 79 người ở quận E tham gia khảo sát
Có 11 người thích bộ phim => Có 68 người không thích => Có 68 kết quả thuận lợi cho biến cố B. Vậy \(P(B) = \frac{{68}}{{79}} \approx 0,861\)
c) Có tổng 415 người của thành phố X tham gia khảo sát. Có 92 người thích bộ phim => Xác suất của biến cố "Người được chọn thích bộ phim trong 415 người của thành phố X" là: \(\frac{{92}}{{415}} \approx 0,22\)
Vậy trong 600 người, số lượng người thích bộ phim khoảng 600.0,22≈132 (người)
d) Có tổng 214 người nữ của thành phố X tham gia khảo sát trong đó có 44 người thích bộ phim => Xác suất của biến cố "Người nữ được chọn thích bộ phim trong 214 người nữ của thành phố X" là: \(\frac{{44}}{{214}} \approx 0,20\)
Vậy chọn ngẫu nhiên 500 người nữ, số lượng người nữ thích bộ phim khoảng 500.0,20≈100 (người)

Vì 5 quả bóng có kích thước và khối lượng giống nhau nên 5 kết quả của phép thử có khả năng xảy ra bằng nhau.
- Biến cố \(A\) xảy ra khi ta lấy được quả bóng có số 5 hoặc 13 nên có 2 kết quả thuận lợi cho \(A\). Xác suất của biến có \(A\) là:
\(P\left( A \right) = \frac{2}{5}\).
- Vì không có quả bóng nào đánh số chia hết cho 3 nên số kết quả thuận lợi của biến cố \(B\) là 0. Xác suất của biến cố \(B\) là
\(P\left( B \right) = \frac{0}{5} = 0\).
- Vì cả 5 quả bóng đều đánh số lớn hơn 4 nên số kết quả thuận lợi của biến cố \(C\) là 5. Xác suất của biến cố \(C\) là
\(P\left( C \right) = \frac{5}{5} = 1\).

Khi lấy 1 tấm thẻ ra khỏi hộp thì số chỉ trên tấm thẻ có thể là: thẻ 3; thẻ 4; thẻ 5; thẻ 6; thẻ 7; thẻ 8; thẻ 9; thẻ 10; thẻ 11; thẻ 12.
Các kết quả cho biến cố \(A\): “ Số ghi trên thẻ lấy ra chia hết cho 3” là thẻ 3; thẻ 3; thẻ 9; thẻ 12.
Các kết quả cho biến cố \(B\): “ Số ghi trên thẻ lấy ra chia hết cho 6” là thẻ 6; thẻ 12.
Có tổng 90 số có 2 chữ số => Có 90 kết quả có thể của hành động này
a) Các kết quả thuận lợi của biến cố A là: 10; 11; 12; 13; 14; 15; 16; 17; 18; 19 => Xác suất của biến cố A là: \(\frac{{10}}{{90}} = \frac{1}{9}\)
b) Các kết quả thuận lợi cho biến cố B là: 16; 26; 36; 49; 64; 81 => Xác suất của biến cố B là: \(\frac{6}{{90}} = \frac{1}{{15}}\)