Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
- Số phần tử của không gian mẫu là: \(C_{21}^2 = 210\)
- Số số chẵn là: 10
- Số số lẻ là: 11
- Để chọn được hai số có tổng là một số chẵn ta cần chọn
+ TH1: 2 số cùng là số chẵn: \(C _{10}^2= 45\) (cách)
+ TH2: 2 số cùng là số lẻ: \({}C_{11}^2 = 55\)
⇨ Xác suất để chọn được hai số có tổng là một số chẵn bằng: \(P = \frac{{45 + 55}}{{210}} = \frac{{10}}{{21}}\)
⇨ Chọn C
3a) Trong 1000 số từ 0 đến 999 có 334 số chia hết cho 3, có dạng 3k, 0 < k < 333.
Suy ra xác suất cần tìm là : \(\frac{334}{1000}\)
b) Trong 1000 số từ 0 đến 999 có 200 số chia hết cho 5, có dạng 5k, 0 < k < 199.
Suy ra xác suất cần tìm là : \(\frac{200}{1000}=\frac{1}{5}\)
Đáp án D
Có n ( Ω ) = 9 . 9 . 8 . 7 = 4536 ;
Gọi số đó là a b c d . Số đó muốn chia hết cho 25 thì điều kiện là cd chia hết cho 25. Từ đó c d ∈ { 25 ; 52 ; 50 ; 05 ; 75 ; 57 } .
TH1: c d ∈ { 25 ; 75 } : cd có 4 cách chọn, a:7 cách; b:7 cách => Có 2.7.7 =98 số.
TH2: c d ∈ { 50 } : cd có 2 cách chọn, a:8 cách chọn, b:7 cách => Có 8.7 = 56 số.
Vậy n(A) = 98 + 56 = 154
⇒ p ( A ) = n ( A ) n ( Ω ) = 154 4536 = 11 342 .
.
Đáp án C
Số số tự nhiên gồm 4 chữ số đôi một khác nhau là 
. Không gian mẫu 
có số phần tử là 
.
Gọi A là biến cố “Số được chọn chia hết cho 25”. Gọi số đó có dạng Chọn thì 
.
* Số đó có dạng 
: Chọn a có 7 cách, chọn b có 7 cách. Suy ra 
số 
thỏa mãn.
* Số đó có dạng 
: Chọn a có 8 cách, chọn b có 7 cách. Suy ra 
số 
thỏa mãn.
* Số đó có dạng 
: Chọn a có 7 cách, chọn b có 7 cách. Suy ra 
số 
thỏa mãn.
Vậy số phần tử của biến cố A là
.
Vậy xác suất cần tính là
.
a) Ω gồm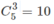 
bộ ba đoạn thẳng khác nhau trong số năm đoạn thẳng đã cho.
b) A gồm các bộ có tổng của hai số lớn hơn số còn lại.
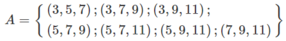
Ta có n(A) = 7
Vậy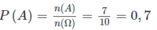 
Chọn B
* Số các số tự nhiên nhỏ hơn 300 là 300 số. Lấy ngẫu nhiên một số tự nhiên nhỏ hơn 300 có suy ra n( Ω ) = 300
* Gọi A là biến cố “số được chọn không chia hết cho 4”, khi đó A ¯ là biến cố “số được chọn
chia hết cho 4”.
* Gọi số tự nhiên nhỏ hơn 300 và chia hết cho 4 là 4n (n ∈ ℕ )
* Ta có 
suy ra 
Do đó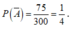 
a, n(Ω)=20C2=190
b,(A)={ 4; 8; 12; 16; 20}
→n(A)=5
vậy P(A)=5 : 190=1:38
Chọn 2 số thì n(A) sao bằng 5 được ạ