Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4
ta có : \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\)\(\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{-1}{z}\)
Ta có: \(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\dfrac{1}{x^3}+3\times\dfrac{1}{x^2}\times\dfrac{1}{y}+3\times\dfrac{1}{x}\times\dfrac{1}{y^2}+\dfrac{1}{y^3}-3\times\dfrac{1}{x^2}\times\dfrac{1}{y}-3\times\dfrac{1}{x}\times\dfrac{1}{y^2}+\dfrac{1}{z^3}\) \(\Leftrightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^3-3\times\dfrac{1}{xy}\times\left(\dfrac{1}{x}+\dfrac{1}{y}\right)+\dfrac{1}{z^3}\)
\(\Leftrightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\left(\dfrac{-1}{z}\right)^3-3\times\dfrac{1}{xy}\times\left(\dfrac{-1}{z}\right)+\dfrac{1}{z^3}\)
\(\Leftrightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=-\dfrac{1}{z^3}+3\times\dfrac{1}{xyz}+\dfrac{1}{z^3}\)
\(\Leftrightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\dfrac{3}{xyz}\Leftrightarrow xyz\left(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}\right)=3\)(ĐPCM)

Bài 4:
Đặt P =\(\dfrac{ab}{a+b}+\dfrac{bc}{b+c}+\dfrac{ca}{c+a}\)
\(P=a-\dfrac{a^2}{a+b}+b-\dfrac{b^2}{b+c}+c-\dfrac{c^2}{c+a}\)
\(P=a+b+c-\left(\dfrac{a^2}{a+b}+\dfrac{b^2}{b+c}+\dfrac{c^2}{c+a}\right)\le a+b+c-\dfrac{\left(a+b+c\right)^2}{2\left(a+b+c\right)}\)
\(P\le a+b+c-\dfrac{a+b+c}{2}=\dfrac{a+b+c}{2}\left(đpcm\right)\)
Dấu "=" xảy ra khi a = b = c
Bài 3 :
\(Ta.có:2x^2+3y^2-2z^2=0\)
\(\Leftrightarrow3y^2=2\left(z^2-x^2\right)=2\left(z-x\right)\left(z+x\right)\)
\(y>0=>3y^2>0;z+x>0\left(x,z>0\right)\)
\(=>z-x>0=>z>x\left(1\right)\)
\(2x^2+3y^2-2z^2=2x^2+y^2=2\left(z^2-y^2\right)\)
\(=>z>y\left(2\right)\)
\(\left(1\right),\left(2\right)=>z>x,y\)
Vậy............................

C1: điều kiện xác định của phương trình 5x+14x−2+x−31+x=05x+14x−2+x−31+x=0 là:
A. x ≠≠1212
B. x ≠≠-1 và x ≠≠1212
C. x ≠≠-1 và x≠−12≠−12
D. x ≠≠-1
C2: bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
A. 2x2 +1<0
B. 0.x +4>0
C. x+33x+2016>0x+33x+2016>0
D. 11x−1<011x−1<0
C3: với x < y ta có:
A. x-5 >y -5
B. 5-2x <5-2y
C. 5-x<5-y
D. 2x-5<2y -5
C4: khi x<0 kết quả rút gọn của biểu thức |−2x|−x+5|−2x|−x+5 là:
A. -3x+5
B. x+5
C. -x+5
D. 3x+5

C1: nghiệm của phương trình 2x+6=1 là:
A. x =-2,5
B. x =2,5
C. x=3,5
D. x=-3,5
C2:Tập nghiệm của phương trình 2x̣̣(x-3)=0
A. S={0}{0}
B. S = {0; 3}
C. S={3}{3}
D. S=∅
C3: Tập nghiệm của phương trình \(\frac{3x-2}{2}=x\)3x−22=x là:
A. S = {2}
B. S={−2}{−2}
C. S=∅
D. S=[1][1]
C4:Tập nghiệm của phương trình x2-16 =0
A. S={16}{16}
B. S={4}{4}
C. S={−4}{−4}
D. S = {-4; 4}
C5: Bất phương trình 2x-3>0. Có nghiệm là:
A. x>1
B. x>1,5
C. xB. x>-1,5
D. x<1,5
C6:Bất phương trình 5x<2x-3 Có nghiệm là:
A. x <-1
B. x > 1
C. x >-0,5
D. x <0,5

TL:
\(A=\left(b^2+c^2-a^2\right)^2-4b^2c^2\)
\(=\left(b^2+c^2-a^2+2bc\right)\left(b^2+c^2-a^2-2bc\right)\)
Đáp án:
Giải thích các bước giải:
a, phân tích thành nhân tử
M = (a^2 + b^2 - c^2)^2 - 4a^2b^2
= (a^2 + b^2 - c^2 - 2ab)(a^2 + b^2 - c^2 + 2ab)
= [(a-b)^2 - c^2][(a+b)^2 - c^2]
= (a-b-c)(a-b+c)(a+b-c)(a+b+c)
b. Nếu a,b,c là số đo độ dài 3 cạnh của tam giác thì ta có:
a-b < c => a-b-c < 0
a+c > b => a+b-b > 0
a+b > c => a+b-c > 0
a+b+c > 0
Vì tích của 1 số âm với 3 số dương luôn nhận được kết quả là số âm
=> (a-b-c)(a-b+c)(a+b-c)(a+b+c) < 0
Vậy chứng tỏ a,b,c là số đo độ dài của tam giác thì M < 0
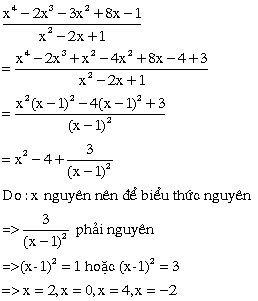
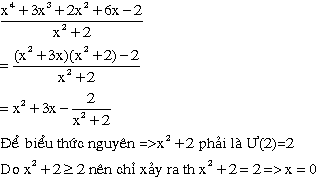 ok bn có thể xem xét mk mk ko chép mạng đâu
ok bn có thể xem xét mk mk ko chép mạng đâu