Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hiện tượng giao thoa xảy ra với hai nguồn sóng kết hợp → hai nguồn cùng phương, cùng pha cùng tần số là hai nguồn kết hợp.
Đáp án B

Chọn B
+ Bước sóng của sóng cm.
+ M và N ngược pha nhau, λ = v / f = 3 giữa M và N có 5 điểm khác ngược pha với M. Các điểm cùng pha liên tiếp nhau thì cách nhau một bước sóng, các điểm ngược pha liên tiếp thì các nhau nửa bước sóng.
Từ hình vẽ ta xác định được MN=5,5 λ = 16 , 5 cm
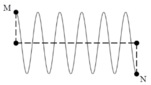

Chọn đáp án C
@ Lời giải:
+ Nếu hai nguồn sóng cùng pha thì những điểm cực tiểu giao thoa nằm tại vị trí: d 2 − d 1 = k + 0,5 λ với k nguyên

Chọn B
+ Với hiện tượng giao thoa hai nguồn kết hợp cùng pha thì trung điểm của đoạn thẳng nối hai nguồn là một cực đại.

Điểm $N$ dao dộng ngược pha với nguồn nằm trên trung trực của $S_{1}S_{2}$ luôn có khoảng cách đến 2 nguồn là $d=(k-\dfrac{1}{2})\lambda$.
Để $N$ gần $S_{1}S_{2}$ nhất thì $k$ min thỏa mãn $d > 4cm=S_{1}S_{2}:2$ hay $k=4$.
Khi đó khoảng cách cần tìm $=\sqrt{d^2-4^2}=\sqrt{5,25^2-4^2}=3,4cm$

Đáp án C
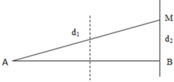
+ Bước sóng: λ = v/f = 0,6/40 = 1,5cm
+ Số cực đại giao thoa trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thoả mãn:
- A B λ < k < A B λ ⇔ - 10 1 , 5 < k < 10 1 , 5 ⇔ - 6 , 67 < k < 6 , 67 ⇒ k = 0 ; ± 1 , ± 2 , . . . . , ± 6
+ Ta có: S A M B = 1 2 A B . M B ⇒ ( S A M B ) m i n ⇔ ( M B ) m i n ⇔ M thuộc cực đại ứng với kmax => d1 – d2 = 6λ = 9cm.
+ Áp dụng định lí Pi – ta – go trong tam giác vuông AMB có:
A B 2 + d 2 2 = d 1 2 ⇔ 10 2 + d 2 2 = ( d 2 + 9 ) 2 ⇒ d 2 = 19 18 c m = M B ⇒ S A M B = 1 2 A B . M B = 1 2 . 10 . 19 18 = 5 , 28 c m 2


D.hai sóng, khi gặp nhau có những điểm chúng luôn tăng cường nhau, có những điểm chúng luôn triệt tiêu nhau.
cảm ơn nhiều nha