Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

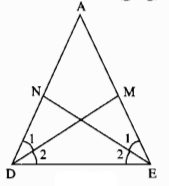
Tam giác ADE có: \(\widehat{\text{D}}=\widehat{E}\)(gt)
\(\widehat{\text{D1}}=\widehat{D2}=\dfrac{1}{2}\widehat{D}\)(Vì DM là tia phân giác)
\(\widehat{\text{E1}}=\widehat{E2}=\dfrac{1}{2}\widehat{E}\)(Vì EN là tia phân giác)
Suy ra:\(\widehat{\text{D1}}=\widehat{D2}=\)\(\widehat{\text{E1}}=\widehat{E2}\)
Xét ∆DNE = ∆EMD, ta có:
\(\widehat{NDE}\widehat{=MED}\)((gt)
DE cạnh chung
\(\widehat{\text{D1}}=\widehat{E2}=\)(chứng minh trên)
Suy ra: ∆DNE = ∆EMD (g.c.g)
Vậy DE = EM (2 cạnh tương ứng).

A B C M N O
Bài này mình thấy chứng minh phần b trước thì ra phần a luôn =)))
b)Tam giác ABC có 2 góc bằng nhau: \(\widehat{ABC}=\widehat{ACB}\) =>Tam giác ABC cân tại A => AB=AC (1)
Tia BM là tia phân giác của góc ABC => \(\widehat{ABM}=\widehat{BM}C=\frac{1}{2}.\widehat{ABC}\)
Tia CN là tia phân giác của góc ACB => \(\widehat{ACN}=\widehat{NCB}=\frac{1}{2}.\widehat{ACB}\)
Mà \(\widehat{ABC}=\widehat{ACB}\) <=> \(\frac{1}{2}.\widehat{ABC}=\frac{1}{2}.\widehat{ACB}\) => \(\widehat{ABM}\)\(=\widehat{ACN}\) (2)
Xét \(\Delta ABM\) và \(\Delta ACN\) có:
- \(\widehat{BAC}\) là góc chung
- AB=AC (suy ra ở (1))
- \(\widehat{ABM}\)\(=\widehat{ACN}\) (suy ra ở (2))
Xét ΔNDE và ΔMED có
\(\widehat{NDE}=\widehat{MED}\)
ED chung
\(\widehat{NED}=\widehat{MDE}\)
Do đó: ΔNDE=ΔMED
Suy ra: ND=ME