TN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LN
1
5 tháng 5 2016
Ta có \(y'=2e^{2x}\sin5x+5e^{2x}\cos5x\)
\(y"=4e^{2x}\sin5x+10e^{2x}\cos5x+10e^{2x}\cos5x-25e^{2x}\sin5x\)
\(=-21e^{2x}\sin5x+20e^{2x}\cos5x\)
Vậy \(y"-4y'+29=-21e^{2x}\sin5x+20e^{2x}\cos5x-8e^{2x}\cos5x+29e^{2x}\sin5x=0\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 5 2020
3.
\(f\left(x+\frac{\pi}{3}\right)=cos\left(x+\frac{\pi}{3}\right)\Rightarrow f'\left(x+\frac{\pi}{3}\right)=-sin\left(x+\frac{\pi}{3}\right)\)
\(f'\left(x-\frac{\pi}{6}\right)=-sin\left(x-\frac{\pi}{6}\right)\)
\(f'\left(0\right)=-sin\left(0\right)=0\)
\(2f'\left(x+\frac{\pi}{3}\right).f'\left(x-\frac{\pi}{6}\right)=2sin\left(x+\frac{\pi}{3}\right)sin\left(x-\frac{\pi}{6}\right)\)
\(=cos\left(\frac{\pi}{2}\right)-cos\left(2x+\frac{\pi}{6}\right)=-cos\left(2x+\frac{\pi}{6}\right)\)
\(f'\left(0\right)-f\left(2x+\frac{\pi}{6}\right)=0-cos\left(2x+\frac{\pi}{6}\right)=-cos\left(2x+\frac{\pi}{6}\right)\)
\(\Rightarrow2f'\left(x+\frac{\pi}{3}\right)f'\left(x-\frac{\pi}{6}\right)=f'\left(0\right)-f\left(2x+\frac{\pi}{6}\right)\) (đpcm)
4.
\(y=3\left(sin^4x+cos^4x\right)-2\left(sin^6x+cos^6x\right)\)
\(=3\left(sin^2x+cos^2x\right)^2-6sin^2x.cos^2x-2\left(sin^2x+cos^2x\right)^3+6sin^2x.cos^2x\left(sin^2x+cos^2x\right)\)
\(=3-2=1\)
\(\Rightarrow y'=0\) ; \(\forall x\)
5.
\(y=\left(\frac{sinx}{1+cosx}\right)^3=\left(\frac{sinx\left(1-cosx\right)}{1-cos^2x}\right)^3=\left(\frac{sinx\left(1-cosx\right)}{sin^2x}\right)^3=\left(\frac{1-cosx}{sinx}\right)^3\)
\(y'=3\left(\frac{1-cosx}{sinx}\right)^2\left(\frac{sin^2x-cosx\left(1-cosx\right)}{sin^2x}\right)=3\left(\frac{1-cosx}{sinx}\right)^2\left(\frac{1-cosx}{sin^2x}\right)=\frac{3\left(1-cosx\right)^3}{sin^4x}\)
\(\Rightarrow y'.sinx-3y=\frac{3\left(1-cosx\right)^3}{sin^3x}-3\left(\frac{1-cosx}{sinx}\right)^3=0\) (đpcm)
TV
1
CM
17 tháng 2 2017
+ sin 2x (x + kπ) = sin (2x + k2π) = sin 2x, (k ∈ Z)
(Do hàm số y = sin x có chu kì 2π).
⇒ Hàm số y = sin 2x tuần hoàn với chu kì π.
+ Hàm số y = sin 2x là hàm số tuần hoàn với chu kì π và là hàm số lẻ.
Bảng biến thiên hàm số y = sin 2x trên [-π/2; π/2]
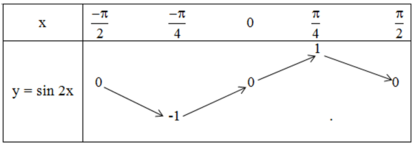
Đồ thị:
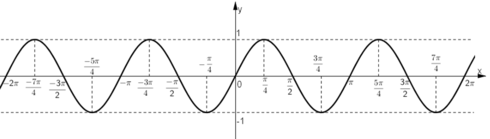
Đồ thị hàm số y = sin 2x.
5 tháng 6 2017
sin^2x.sin^2x+cos^2x.cos^2x=1-1/2sin^2(2x)
<=>(1-cos2x)^2/4+(1+cos2x)^2/4=1-1/2sin^2(2x)
<=>(cos^2(2x)+1)/2=1-1/2sin^2(2x)
cos^2(2x)+1=2- sin^2(2x)
cos^2(2x)+sin^2(2x)=1( luôn đúng)
đpcm
HT
1
VB
5 tháng 5 2016
Ta có \(y'=\frac{\cos\left(\ln x\right)-\sin\left(\ln x\right)}{x}\)
\(\Rightarrow y"=\frac{x.\frac{-\sin\left(\ln x\right)-\cos\left(\ln x\right)}{x}-\left[\cos\left(\ln x\right)-\sin\left(\ln x\right)\right]}{x^2}=\frac{-2\cos\left(\ln x\right)}{x^2}\)
Ta có :
\(y+xy'+x^2y"=\sin\left(\ln x\right)+\cos\left(\ln x\right)+\cos\left(\ln x\right)-\sin\left(\ln x\right)-2\cos\left(\ln x\right)=0\)
5 tháng 5 2016
Ta có :
\(y'=\sin x+x\cos x\)
\(y"=\cos x+\cos x-x\sin x=2\cos x-x\sin x\)
Vậy \(xy-2\left(y'-\sin x\right)+xy"=x^2\sin x-2\left(\sin x-x\cos x-\sin x\right)+2x\cos x-x^2\sin x=0\)