Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
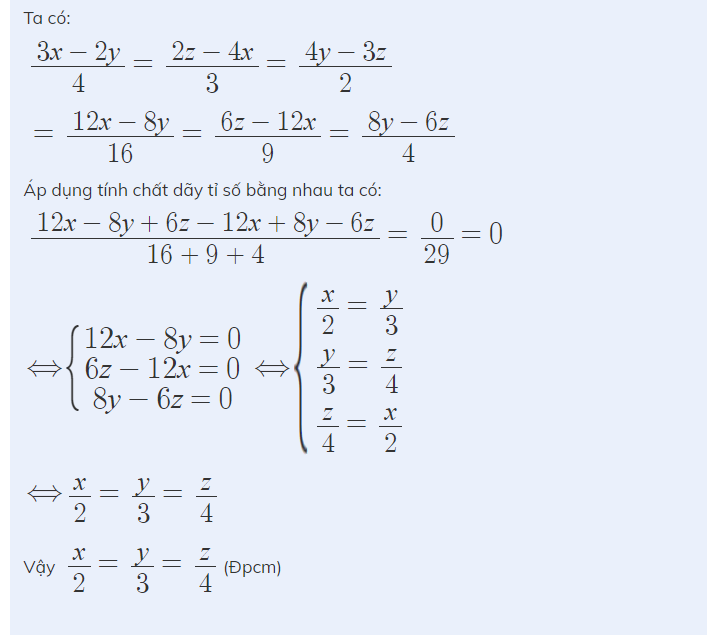

a, Chứng minh \(x^3+y^3+z^3=\left(x+y\right)^3-3xy.\left(x+y\right)+z^3\)
Biến đổi vế phải thì ta phải suy ra điều phải chứng minh
b, Ta có: \(a+b+c=0\)thì
\(a^3+b^3+c^3==\left(a+b\right)^3-3ab\left(a+b\right)+c^3=-c^3-3ab\left(-c\right)+c^3=3abc\)
( Vì \(a+b+c=0\)nên \(a+b=-c\))
Theo giả thuyết \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\)
\(\Rightarrow\frac{1}{x^3}+\frac{1}{y^3}+\frac{1}{z^3}=\frac{3}{xyz}\)
Khi đó \(A=\frac{yz}{x^2}+\frac{xz}{y^2}+\frac{xy}{z^2}\)
\(=\frac{xyz}{x^3}+\frac{xyz}{y^3}+\frac{xyz}{z^3}\)
\(=xyz\left(\frac{1}{x^3}+\frac{1}{y^3}+\frac{1}{z^3}\right)\)
\(=xyz.\frac{3}{xyz}=3\)

Ta có
a3 + b3 + c3 - 3abc = 0
<=> (a + b)3 + c3 - 3ab(a + b) - 3abc = 0
<=> (a + b + c)(a2 + b2 + c2 + 2ab - ac - bc) - 3ab(a + b + c) = 0
<=> (a + b + c)(a2 + b2 + c2 - ab - ac - bc) = 0
<=> (a2 + b2 + c2 - ab - ac - bc) = 0
<=> (a2 - 2ab + b2) + (a2 - 2ac - c2) + (b2 - 2bc + c2) = 0
<=> (a - b)2 + (a - c)2 + (b - c)2 = 0
<=> a = b = c
=> P = (1 + 1)(1 + 1)(1 +1) = 8