K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 1 2024
Bài 2:
a: \(\left(x-8\right)\left(x^3+8\right)=0\)
=>\(\left[{}\begin{matrix}x-8=0\\x^3+8=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=8\\x^3=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
b: \(\left(4x-3\right)-\left(x+5\right)=3\left(10-x\right)\)
=>\(4x-3-x-5=30-3x\)
=>3x-8=30-3x
=>6x=38
=>\(x=\dfrac{38}{6}=\dfrac{19}{3}\)
Bài 6:
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
b: Ta có: HB=HC
H nằm giữa B và C
Do đó: H là trung điểm của BC
=>\(HB=HC=\dfrac{8}{2}=4\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-4^2=9\)
=>\(AH=\sqrt{9}=3\left(cm\right)\)
c: Ta có: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H
d: Ta có: HD=HE
HE<HC(ΔHEC vuông tại E)
Do đó:HD<HC
5 tháng 5 2016
a.
(x^2 + y^2 - 2xy) + (x^2 + y^2 + 2xy)
= x^2 + y^2 - 2xy + x^2 + y^2 + 2xy
= (x^2 + x^2) + (y^2 + y^2) + (2xy - 2xy)
= 2x^2 + 2y^2
b.
(x^2 + y^2 - 2xy) - (x^2 + y^2 + 2xy)
= x^2 + y^2 - 2xy - x^2 - y^2 - 2xy
= (x^2 - x^2) + (y^2 - y^2) - (2xy + 2xy)
= -4xy
NN
14 tháng 7 2016
Ta có công thức (a+b)2=(a+b)(a+b)=a2+2ab+b2
Vậy a2+2ab+b2 cũng giống như x2+2xy+y2(chỉ khác ab;xy)
Do đó ta có:
A=x2+2xy+y2-4x-4y+1
A=(x+y)2-4.(x+y)+1
A=32-4.3+1
A=9-12+1
A=-2
Vậy A=-2
BT
1
13 tháng 1 2019
\(P=2x^2y+2xy^2-2xy+5\)
\(P=2xy\left(x+y-1\right)+5\)
Thay x + y = 1 ta có :
\(P=2xy\left(1-1\right)+5\)
\(P=2xy\cdot0+5\)
\(P=5\)
Vậy....
19 tháng 9 2018
M + N = \(x^2-2xy+y^2\)+\(y^2+2xy+x^2+1\)
= \(\left(x^2+x^2\right)+\left(-2xy+2xy\right)+\left(y^2+y^2\right)+1\)
= \(2x^2+2y^2+1\)
M - N = \(x^2-2xy+y^2-y^2+2xy+1\)
= \(\left(x^2+x^2\right)+\left(-2xy+2xy\right)+\left(y^2-y^2\right)+1\)
= \(2x^2+1\)
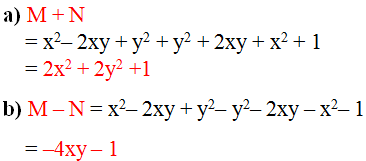
Thay \(x+y=1\) vào biểu thức \(A=x^2+2xy+y^2+2022\) ta được:
\(A=\left(1\right)^2+2.1.1+\left(1\right)^2+2022\)
\(A=1+2.1.1+1+2022\)
\(A=1+2+1+2022\) \(=2026\)
Vậy: \(x+y=1\) thì biểu thức \(A=x^2+2xy+y^2+2022\) là \(2026\)