Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thôi em không cần bài này nữa đâu mọi người :) em biết làm rồi :) //chờ mãi chả ai làm giúp :(( buồn mọi người ghia ớ :'( //

Ta có:\(P=x^3\left(z-y^2\right)+y^3x-y^3z^2+z^3y-z^3x^2+x^2y^2z^2-xyz\)
\(\Rightarrow P=x^3\left(z-y^2\right)+x^2y^2z^2-x^2z^3-\left(y^3z^2-z^3y\right)+y^3x-xyz\)
\(\Rightarrow P=x^3\left(z-y^2\right)+x^2z^2\left(y^2-z\right)-yz^2\left(y^2-z\right)+xy\left(y^2-z\right)\)
\(\Rightarrow P=\left(y^2-z\right)\left(x^2z^2-x^3-yz^2+xy\right)\)
\(\Rightarrow P=\left(y^2-z\right)\left(x^2z^2-x^3+xy-yz^2\right)\)
\(\Rightarrow P=\left(y^2-z\right)\left(x^2\left(z^2-x\right)+y\left(x-z^2\right)\right)\)
\(\Rightarrow P=\left(y^2-z\right)\left(x^2\left(z^2-x\right)-y\left(z^2-x\right)\right)\)
\(\Rightarrow P=\left(y^2-z\right)\left(z^2-x\right)\left(x^2-y\right)\)
\(\Rightarrow P=abc\)
Vì a, b, c là hằng số nên P có giá trị không phụ thuộc vào x, y, z

1) Biến đồi tương đương:
\(\left(x^2+y^2\right)^2\ge8\left(x-y\right)^2\)
\(\Leftrightarrow\left(x^2+y^2\right)^2\ge8xy\left(x-y\right)^2\)
\(\Leftrightarrow\left(x^2-4xy+y^2\right)^2\ge0\)(đúng)
2) Sửa đề: \(\frac{1}{1+x^2}+\frac{1}{1+y^2}\ge\frac{2}{1+xy}\left(\text{với }xy\ge1\right)\)
\(\Leftrightarrow\frac{\left(x-y\right)^2\left(xy-1\right)}{\left(x^2+1\right)\left(y^2+1\right)\left(xy+1\right)}\ge0\) (đúng)

a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
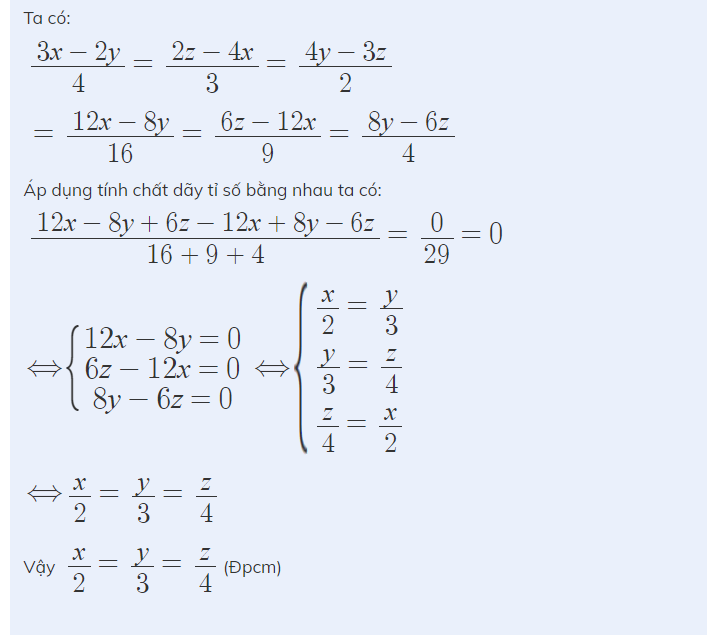

Ta có: (a2+b2)(x2+y2)=(ax+by)2
\(\Leftrightarrow\)a2x2+a2y2+b2x2+b2y2=a2x2+2abxy+b2y2
\(\Leftrightarrow\)a2y2-2abxy+b2x2=0
\(\Leftrightarrow\)(ay-bx)2=0
\(\Leftrightarrow\)ay=bx
\(\Leftrightarrow\)\(\frac{a}{x}\)=\(\frac{b}{y}\)
#)Giải :
\(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(\Rightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+2abxy+b^2y^2\)
\(\Rightarrow a^2y^2+b^2x^2=2abxy\)
\(\Rightarrow a^2y^2+b^2x^2-2abxy=0\)
\(\Rightarrow\left(ay-bx\right)^2=0\)
\(\Rightarrow ay-bx=0\)
\(\Rightarrow ay=bx\)
\(\Rightarrow\frac{a}{x}=\frac{b}{y}\)(theo tính chất tỉ lệ thức)
\(\Rightarrowđpcm\)

1) \(VT=x^3+x^2y-x^2y-xy^2+xy^2+y^3=x^3+y^3=VP\)
2) \(VP=x^2+xy-xy-y^2=x^2-y^2=VT\)
3) \(VP=x^2+2\cdot x\cdot1+1=x^2+2x+1=VT\)
4) \(VP=x^3+x^2y+xy^2-x^2y-xy^2-y^3=x^3-y^3=VT\)
1, \(\left(x^2-xy+y^2\right)\left(x+y\right)=x^3+y^3\\ x^3+x^2y-x^2y-xy^2+xy^2+y^3=x^3+y^3\\ x^3+y^3=x^3+y^3\left(đúng\right)\)Vậy ta được đpcm
2, \(x^2-y^2=\left(x-y\right)\left(x+y\right)\\ x^2-y^2=x^2+xy-xy-y^2\\ x^2-y^2=x^2-y^2\left(đúng\right)\)Vậy ta được đpcm
3, \(x^2+2x+1=\left(x+1\right)^2\\ x^2+2x+1=\left(x+1\right)\left(x+1\right)\\ x^2+2x+1=x^2+x+x+1\\ x^2+2x+1=x^2+2x+1\left(đúng\right)\)Vậy ta được đpcm
4, \(x^3-y^3=\left(x-y\right)\left(x^2+xy+y^2\right)\\ x^3-y^3=x^3+x^2y+xy^2-x^2y-xy^2-y^3\\ x^3-y^3=x^3-y^3\left(đúng\right)\)Vậy ta được đpcm

a) y(x2-y2)(x2+y2)-y(x4-y4)=y[(x2)2-(y2)2] - y(x4-y4)=y(x4-y4)-y(x4-y4)=0
vậy giá trị biểu thức không phụ thuộc vào biến (đpcm)
b) \(\left(\frac{1}{3}+2x\right)\left(4x^2-\frac{2}{3}x+\frac{1}{9}\right)-\left(8x^3-\frac{1}{27}\right)\)
\(=\left[\left(2x\right)^3+\left(\frac{1}{3}\right)^3\right]-\left(8x^3-\frac{1}{27}\right)=8x^3+\frac{1}{27}-8x^3+\frac{1}{27}=\frac{1}{54}\)
vậy giá trị biểu thức không phụ thuộc vào biến (đpcm)
c) (x - 1)^3 - (x - 1)(x^2 + x + 1) - 3(1 - x)x
= (x - 1)(x^2 + x + 1) - (x - 1)(x^2 + x + 1) - 3x(1 - x)
= x^3 - 3x^2 + 3x - 1 - x^3 + 1 - 3x + 3x^2
= 0 (đpcm)
Cậu ơi, sao lại ra được bước thứ 2 vậy?