Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(P=\left(x^4-8x^3+16x^2\right)+12x^2-48x+35\)
\(=\left(x^2-4x\right)^2+12\left(x^2-4x\right)+36-1\)
\(=\left(x^2-4x+6\right)^2-1\)
\(=\left[\left(x-2\right)^2+2\right]^2-1\)
\(\ge2^2-1=3\)
Cách khác \(P=\left(x-2\right)^2\left[\left(x-2\right)^2+4\right]+3\ge3\)
Đẳng thức xảy ra khi \(x=2.\)
b, \(xy\le\frac{\left(x+y\right)^2}{4}=9\)
Áp dụng bđt Co6si: \(\frac{1}{x^2}+\frac{1}{y^2}\ge2\sqrt{\frac{1}{x^2}.\frac{1}{y^2}}=\frac{2}{xy}\)
\(Q\ge\frac{102}{xy}+xy=xy+\frac{81}{xy}+\frac{21}{xy}\ge2\sqrt{xy.\frac{81}{xy}}+\frac{21}{9}=\frac{61}{3}.\)
Dấu bằng xảy ra khi \(x=y=3.\)

\(A=\dfrac{1-\sqrt{x}+x}{\sqrt{x}}\\ =\dfrac{\left(1-\sqrt{x}+x\right)\sqrt{x}}{x}\\ =\dfrac{\sqrt{x}-x+x\sqrt{x}}{x}\)
lm tiếp...

coi như giải hệ pt
\(\hept{\begin{cases}y=x+1\left(1\right)\\y^2-3y\sqrt{x}+2x=0\left(2\right)\end{cases}}\)
\(\left(2\right)\Leftrightarrow\left(y^2-3\sqrt{x}.y+\frac{9x}{4}\right)=\frac{9x}{4}-2x=\frac{x}{2}\\ \)
\(\left(y-\frac{3\sqrt{x}}{2}\right)^2=\left(\frac{\sqrt{x}}{2}\right)^2\Rightarrow\orbr{\begin{cases}y=\frac{3\sqrt{x}}{2}-\frac{\sqrt{x}}{2}=\sqrt{x}\\y=\frac{3\sqrt{x}}{2}+\frac{\sqrt{x}}{2}=2\sqrt{x}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x}=x+1\left(3\right)\\2\sqrt{x}=x+1\left(4\right)\end{cases}}\)
\(\left(3\right)\Leftrightarrow\orbr{\begin{cases}\left(\sqrt{x}-\frac{1}{2}\right)^2=\frac{1}{4}-1\left(vonghiem\right)\\\left(\sqrt{x}-1\right)^2=0\Rightarrow\sqrt{x}=1\Rightarrow x=1\end{cases}}\)
Vậy chỉ có điểm x=1; y=2 thỏa mãn

Sủ dụng: \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b};\text{ }ab\le\frac{\left(a+b\right)^2}{4}\)
\(xy\le\frac{\left(x+y\right)^2}{4}\le\frac{1}{4}\)
\(P=\frac{1}{x^2+y^2}+\frac{1}{2xy}+4xy+\frac{1}{4xy}+\frac{5}{4xy}\)
\(\ge\frac{4}{x^2+y^2+2xy}+2\sqrt{4xy.\frac{1}{4xy}}+\frac{5}{4.\frac{1}{4}}\)
\(=\frac{4}{\left(x+y\right)^2}+2+5\)
\(\ge4+2+5=11\)
Dấu bằng xảy ra khi \(x=y=\frac{1}{2}\)
\(-------\)
Chứng minh bổ đề: \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\) \(\left(i\right)\) (với \(a,b>0\) )
Bđt \(\left(i\right)\) tương đương với bđt sau:
\(\left(a+b\right)\left(\frac{1}{a}+\frac{1}{b}\right)\ge4\) \(\left(ii\right)\)
Ta cần chứng minh bđt \(\left(ii\right)\) luôn đúng với mọi \(a,b>0\)
Thật vậy, ta áp dụng bđt \(Cauchy\) loại hai cho từng bộ số gồm hai số không âm đề giải quyết bài toán trơn tru như sau:
\(\frac{1}{a}+\frac{1}{b}\ge2\sqrt{\frac{1}{ab}}\) \(\left(1\right)\)
\(a+b\ge2\sqrt{ab}\) \(\left(2\right)\)
Nhân từng vế \(\left(1\right)\) và \(\left(2\right)\) , ta suy ra điều phải chứng minh.
Vì bđt \(\left(ii\right)\) được chứng minh nên kéo theo bđt \(\left(i\right)\) luôn đúng với mọi \(a,b>0\)
Đẳng thức xảy ra khi và chỉ khi \(a=b\)
\(-------\)
Quay trở về bài toán, ta có:
\(1\ge x+y\ge2\sqrt{xy}\)
\(\Rightarrow\) \(\sqrt{xy}\le\frac{x+y}{2}\le\frac{1}{2}\)
nên suy ra được \(xy\le\frac{1}{4}\)
\(P=\frac{1}{x^2+y^2}+\frac{2}{xy}+4xy=\left(\frac{1}{x^2+y^2}+\frac{1}{2xy}\right)+\left(\frac{1}{4xy}+4xy\right)+\frac{5}{4xy}\)
Áp dụng bđt \(\left(i\right)\) cho biểu thức đầu tiên, bđt Cauchy cho biểu thức thứ hai và với chú ý rằng \(xy\le\frac{1}{4}\) , ta được:
\(P\ge\frac{4}{\left(x+y\right)^2}+2\sqrt{\frac{1}{4xy}.4xy}+\frac{5}{4.\frac{1}{4}}=4+2+5=11\)
Dấu \("="\) xảy ra khi và chỉ khi \(x=y=\frac{1}{2}\) (bạn cần làm rõ khúc này nha)
Vậy, \(P_{min}=11\) \(\Leftrightarrow\) \(x=y=\frac{1}{2}\)

\(A=\dfrac{x^2+2x+17}{2\left(x+1\right)}=\dfrac{x^2-6x+9+8x+8}{2\left(x+1\right)}\\ =\dfrac{\left(x-3\right)^2+8\left(x+1\right)}{2\left(x+1\right)}=\dfrac{\left(x-3\right)^2}{2\left(x+1\right)}+4\)
Vì \(\left(x-3\right)^2\ge0;2\left(x+1\right)>0\) (do \(x>-1\))
\(\Rightarrow\dfrac{\left(x-3\right)^2}{2\left(x+1\right)}\ge0\Leftrightarrow A=\dfrac{\left(x-3\right)^2}{2\left(x+1\right)}+4\ge4\)
Dấu "=" xảy ra khi \(x=3\)
Vậy....

\(1,A=\frac{1}{x^2+y^2}+\frac{1}{xy}=\frac{1}{x^2+y^2}+\frac{1}{2xy}+\frac{1}{2xy}\)
\(\ge\frac{4}{\left(x+y^2\right)}+\frac{1}{\frac{\left(x+y\right)^2}{2}}\ge\frac{4}{1}+\frac{2}{1}=6\)
Dấu "=" <=> x= y = 1/2
\(2,A=\frac{x^2+y^2}{xy}=\frac{x}{y}+\frac{y}{x}=\left(\frac{x}{9y}+\frac{y}{x}\right)+\frac{8x}{9y}\ge2\sqrt{\frac{x}{9y}.\frac{y}{x}}+\frac{8.3y}{9y}\)
\(=2\sqrt{\frac{1}{9}}+\frac{8.3}{9}=\frac{10}{3}\)
Dấu "=" <=> x = 3y

Ta có: \(P=\frac{x^2+y^2}{x-y}=\frac{\left(x-y\right)^2+2xy}{x-y}=\left(x-y\right)+\frac{2xy}{x-y}\)
\(=x-y+\frac{16}{x-y}\ge2.4=8\)
Đặt \(t=x^2+y^2\) thì ta có :
\(P^2=\frac{\left(x^2+y^2\right)^2}{\left(x-y\right)^2}=\frac{t^2}{t-16}=\frac{1}{\frac{t-16}{t^2}}=\frac{1}{-\frac{16}{t^2}+\frac{1}{t}}=\frac{1}{-16\left(\frac{1}{t}-\frac{1}{32}\right)^2+\frac{1}{64}}\ge\frac{1}{\frac{1}{64}}=64\)
\(\Rightarrow P\ge8\). Đẳng thức xảy ra khi \(\hept{\begin{cases}x^2+y^2=32\\xy=8\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x=2+2\sqrt{2}\\y=-2+2\sqrt{3}\end{cases}}\)

\(B=\dfrac{xy}{xy}+\dfrac{\left(x-y\right)x}{x\left(x-y\right)}-\dfrac{y\left(x-y\right)}{y\left(x-y\right)}=1\)
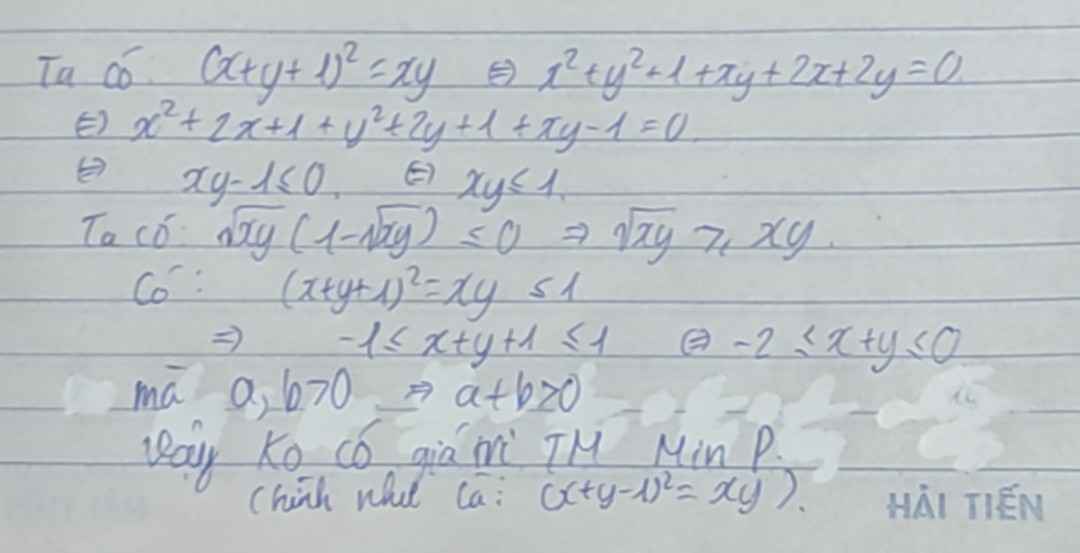
Áp dụng BĐT Cauchy ta có:
P = \(x^2+y^2+\dfrac{33}{xy}\) \(\ge\) \(\dfrac{\left(x+y\right)^2}{2}+\dfrac{33}{x+y}\) = \(\dfrac{4^2}{2}+\dfrac{33}{4}=\dfrac{65}{4}\)
=> Dấu = xảy ra <=> \(\left\{{}\begin{matrix}x+y=4\\x=y\end{matrix}\right.\) <=> \(x=y=2\)
Vậy ...............................