Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(B=x\left(x+y\right)\left(x-y\right)\left(x+2y\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+2xy-xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)^2-2y^2\left(x^2+xy\right)+y^4\)
\(=\left(x^2+xy-y^2\right)^2\)
b: \(C=\left(x-y\right)\left(x-4y\right)\left(x-2y\right)\left(x-3y\right)+y^4\)
\(=\left(x^2-5xy+4y^2\right)\left(x^2-5xy+6y^2\right)+y^4\)
\(=\left(x^2-5xy\right)^2+10y^2\left(x^2-5xy\right)+25y^4\)
\(=\left(x^2-5xy+5y^2\right)^2\)

ta có (x+y)(x+2y)(x+3y)(x+4y)+y^4
=(x+y)(x+4y)(x+2y)(x+3y)+y^4
=(x^2+5xy+4y^2)(x^2+5xy+6y^2)+y^4
đặt x^2+5xy=a
<=>A=a(a+2y^2)+y^4
=a^2+2.a.y^2+y^4
=(a+y^2)^2
là scp

A=(x+y)(x+2y)(x+3y)(x+4y)+y4
A=(x+y)(x+4y).(x+2y)(x+3y)+y4
A=(x2+5xy+4y2)(x2+5xy+6y2)+y4
A=(x2+5xy+ 5y2 - y2 )(x2+5xy+5y2+y2)+y4
A=(x2+5xy+5y2)2-y4+y4
A=(x2+5xy+5y2)2
Do x,y,Z nen x2+5xy+5y2 Z
A là số chính phương
a) Ta có: A= (x+y)(x+2y)(x+3y)(x+4y)+y4
= (x2 + 5xy + 4y2)( x2 + 5xy + 6y2) + y2
Đặt x2 + 5xy + 5y2 = h ( h thuộc Z):
A = ( h - y2)( h + y2) + y2 = h2 – y2 + y2 = h2 = (x2 + 5xy + 5y2)2
Vì x, y, z thuộc Z nên x2 thuộc Z, 5xy thuộc Z, 5y2 thuộc Z . Suy ra x2 + 5xy + 5y2 thuộc Z
Vậy A là số chính phương.

A=\([\)(x+y)(x+4y)\(][\)(x+2y)(x+3y)]+y4
=(x2+4xy+xy+4y2)(x2+3xy+2xy+6y2)+y4
=(x2+5xy+4y2)(x2+5xy+6y2)+y4
=(x2+5xy+5y2-y2)(x2+5xy+5y2+y2)+y4
=(x2+5xy+5y2)2-y4+y4
=(x2+5xy+5y2)2
vậy A là số chính phương vs \(\forall\) x,y\(\in\)R

\(A=\left[\left(x+y\right)\left(x+4y\right)\right]\left[\left(x+2y\right)\left(x+3y\right)\right]+y^4\\ A=\left(x^2+5xy+4y^2\right)\left(x^2+5xy+6y^2\right)+y^4\\ A=\left(x^2+5xy+5y^2-y^2\right)\left(x^2+5xy+5y^2+y^2\right)+y^4\\ A=\left(x^2+5xy+5y^2\right)^2-y^4+y^4=\left(x^2+5xy+5y^2\right)^2\left(Đpcm\right)\)
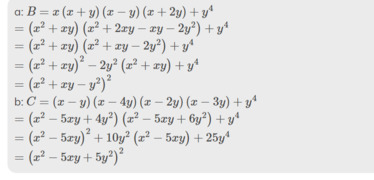
=[(x+1)(x+6)][(x+3)(x+4)]+9
Sau khi nhân thì sẽ có kết quả sau : =(x2+7x+6)(x2+7x+12)+9 . Sẽ đặt ẩn phụ là (x2+7x+6) = a . suy ra a2+6a+9=(x+3)2 rồi lại thay ngược lại thì có kết quả cuối cùng là (x2+7x+9)2=>M là số chính phương