Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét 2 tam giác vuông OAC và tam giác OBD có:
OA = OB (gt)
O là góc chung
suy ra tam giác OAC = tam giác OBD (cạnh góc vuông - góc nhọn kề cạnh ấy)
b) Ta có : OD = OA + AD
OC = OB + BC
mà OD = OC (vì tam giác OAC = tam giác OBD)
OA = OB ( gt)
suy ra AD = BC
Xét 2 tam giác vuông ADI và tam giác BCI có:
AD = BC (cmt)
góc D = góc C (vì tam giác OAC = tam giác OBD)
suy ra tam giác ADI và tam giác BCI (cạnh goác vuông - góc nhọn kề cạnh ấy)
suy ra IA = IB (2 cạnh tương ứng)
c)Xét 2 tam giác vuông OAI và tam giác OBI có:
OI là cạnh chung
OA = OB (gt)
suy ra tam giác OAI = tam giác OBI (2 cạnh góc vuông)
suy ra góc O1 = góc O2 (2 góc tương ứng)
suy ra OI là tia phân giác của góc xOy
Cái chỗ A1, A2, B1, B2 bạn đừng kí hiệu vào bài làm nhé!
Mình nhầm tí!

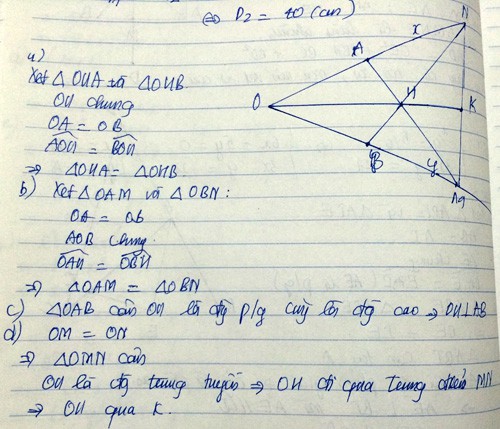
+) Xét tg ONB và OMA có
OB= OA (gt)
Góc O chung
Góc B = góc A(=90)
=> ∆ OMA (ch - gn)
=> />+) Ta có OA + AN = ON
OB+ BM= OM
Mà OA= OB
/>=> AN = BM
+) XÉT ∆OAH và ∆ OBH
OH cạnh cchung
OA= OB
góc A = góc B
=>∆ OAH= ∆ OBH( cho CGV)
=> AOH= BOH
=> OH là phân giác xOy
ta có (cmt)
=> ∆ ONM cân tại O
OI là trung tuyến => OI là đường cao
OI vuông góc NM(1)
Ta có MA, NB lần lượt vuông góc với Ox, Oy
MA cắt NB tại H
=> H là trực tâm của ∆OMN
=> OH vuông góc NM(2)
từ (1)(2)=> O , H , I thẳng hàng ( qua O chỉ kẻ đc duy nhất 1 đường thẳng vuông góc NM)
x O y A B z t m n C p q
a)TA CÓ \(\widehat{OBn}+\widehat{BOA}=90^o+90^o=180^o\)
HAI GÓC \(\widehat{OBn}\)VÀ\(\widehat{BOA}\)Ở VỊ TRÍ TRONG CÙNG PHÍA BÙ NHAU
\(\Rightarrow mn//Ox\)
b) VÌ \(mn//Ox\)
\(\Rightarrow\widehat{BCA}=\widehat{CAx}=90^O\)
\(\Rightarrow\widehat{BCA}=90^O\)
C) TÍNH TIA PHÂN QIACS RỒI CM NHA
GIẢI LUÔN
x o y z t m n p q B A C 1 1
C) Vì TIA OP LÀ TIA PHÂN GIÁC CỦA \(\widehat{xOy}\)
\(\Rightarrow\widehat{yOp}=\widehat{pOx}=\widehat{\frac{xOy}{2}}=\frac{90^o}{2}=45^o\)
Vì TIA Oq LÀ TIA PHÂN GIÁC CỦA \(\widehat{BCA}\)
\(\Rightarrow\widehat{BCq}=\widehat{qCA}=\frac{\widehat{BCA}}{2}=\frac{90^o}{2}=45^0\)
XÉT \(\Delta ZAQ\)
CÓ \(\widehat{Q_1}+\widehat{A}+\widehat{C_1}=180^o\)
THÂY\(\widehat{Q_1}+90^o+45^o=180^o\)
\(\Rightarrow\widehat{Q_1}=45^o\)
\(\Rightarrow\widehat{Q_1}=\widehat{POX}=45^o\)
HAI GÓC\(\widehat{Q_1}\)VÀ \(\widehat{POX}\)Ở VỊ TRÍ ĐỒNG VỊ BẰNG NHAU
\(\Rightarrow Oq//Op\)