TT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 9 2018
\(a)\)\(M=x^3-3xy\left(x-y\right)-y^3-x^2+2xy-y^2\) ( đề nhầm đúng ko bn )
\(M=\left(x^3-3x^2y+3xy^2-y^3\right)-\left(x^2-2xy+y^2\right)\)
\(M=\left(x-y\right)^3-\left(x-y\right)^2\)
\(M=7^3-7^2\)
\(M=294\)
Chúc bạn học tốt ~
NT
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
13 = (\(x+y\))3 = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y3 = \(x^3\)+y3+3\(xy\)(\(x+y\))
1 = \(x^3\)+y3+3\(xy\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\)y + 3\(xy\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
H
14 tháng 7 2017
Giải:
a) \(M=x^3-3xy\left(x-y\right)-y^3-x^2+2xy-y^2\)
\(\Leftrightarrow M=\left[x^3-3xy\left(x-y\right)-y^3\right]-\left(x^2-2xy+y^2\right)\)
\(\Leftrightarrow M=\left(x-y\right)^3-\left(x-y\right)^2\)
Thay \(x-y\) vào, được:
\(M=7^3-7^2=294\)
Vậy ...
b) \(N=x^2\left(x+1\right)-y^2\left(y-1\right)+xy-3xy\left(x-y+1\right)-95\)
\(\Leftrightarrow N=x^3+x^2-y^3+y^2+xy-3xy-3xy\left(x-y\right)-95\)
\(\Leftrightarrow N=x^3+x^2-y^3+y^2-2xy-3xy\left(x-y\right)-95\)
\(\Leftrightarrow N=\left[x^3-y^3-3xy\left(x-y\right)\right]+\left(x^2-2xy+y^2\right)-95\)
\(\Leftrightarrow N=\left(x-y\right)^3+\left(x-y\right)^2-95\)
Thay \(x-y\) vào, được:
\(N=7^3+7^2-95=297\)
Vậy ...
Chúc bạn học tốt!
19 tháng 7 2019
Đề a,b bạn ghi mik ko hiểu
c)Ta có : \(x+y=a=>x^2+y^2+2xy=a^2\)
Mà \(x^2+y^2=b\)nên\(b+2xy=a^2=>xy=\frac{a^2-b}{2}\)
\(x^3+y^3=\left(x+y\right)\left(x^2+y^2-xy\right)\)
Thay \(x+y=a\) ; \(x^2+y^2=b\)và \(xy=\frac{a^2-b}{2}\)ta có : \(x^3+y^3=a\left(b-\frac{a^2-b}{2}\right)=ab-\frac{a^3-ab}{2}\)
14 tháng 7 2017
a. Có \(x+y=2\Rightarrow x^2+2xy+y^2=4\Rightarrow x^2+y^2=4-2.\left(-3\right)=10\)
\(x^4+y^4=\left(x^2\right)^2+\left(y^2\right)^2=\left(x^2+y^2\right)^2-2x^2y^2\)
\(=10^2-2.\left(-3\right)^2=82\)
b. Ta có \(x+y=1\Rightarrow x^2+y^2=1-2xy\)
\(x^3+y^3+3xy=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\)
\(=1.\left(1-2xy-xy\right)+3xy=1\)
Các câu còn lại tương tự
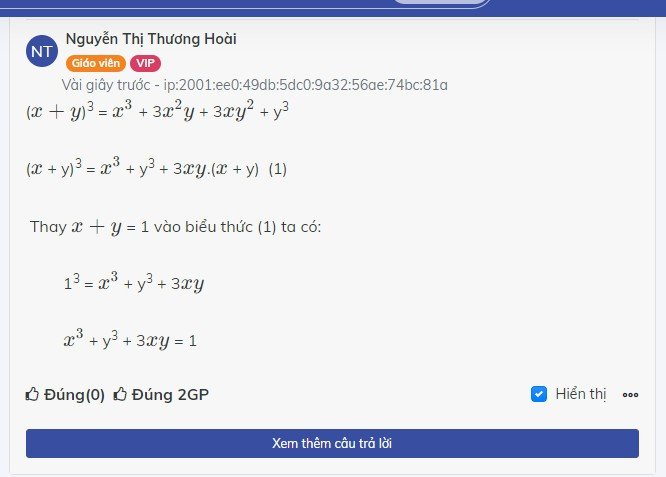
Nhầm đoạn cuối
\(A=\left(5+y-y\right)^3+\left(5+y-y\right)^2=5^3+5^2=150\)
x\(^3\)+ x\(^2\) -y\(^3\)+ y\(^2\)+xy -3x\(^2\)y +3xy\(^2\)-3xy=
=(x\(^3\)+ y\(^3\)-3x\(^2\)y+3xy\(^2\))+ (x\(^2\)-2xy +y\(^2\))= (x-y)\(^3\) +(x-y)\(^2\)= 5\(^3\)+ 5\(^2\)=125 + 25=150