Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\)
\(\Leftrightarrow\frac{yz+zx+xy}{xyz}=0\) (Quy đồng)
\(\Rightarrow yz+zx+xy=0\)
Vì:
\(\left(x^2y^2+y^2z^2+z^2x^2\right)^2=0\)
\(2\left(x^4y^{ }^4+y^4z^4+z^4x^4\right)=0\)
Nên.....(tự kết luận nha)
giải chi tiết ( vì sao ) đoạn dưới đây = 0 hộ mk vs :
vì \(\left(x^2y^2+y^2z^2+z^2x^2\right)^2=0\)
\(2\left(x^4y^4+y^4z^4+z^4x^4\right)=0\)

Ta có:
\(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2=\left(y+z-2x\right)^2+\left(z+x-2y\right)^2+\left(x+y-2z\right)^2\)
\(\Rightarrow2x^2+2y^2+2z^2-2xy-2yz-2zx=6x^2+6y^2+6z^2-6xy-6yz-6zx\)
\(\Rightarrow4x^2+4y^2+4z^2-4xy-4yz-4zx=0\)
\(\Rightarrow2x^2+2y^2+2z^2-2xy-2yz-2zx=0\)
\(\Rightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}\left(x-y\right)^2=0\\\left(y-z\right)^2=0\\\left(z-x\right)^2=0\end{cases}}\Rightarrow x=y=z\)

Bn có thể tham khảo link này:
https://olm.vn/hoi-dap/detail/9056136271.html
#Hok_tốt

Bạn tự tách hđt nhé! Gõ mỏi tay :v~
\(\left(y-z\right)^2+\left(z-x\right)^2+\left(x-y\right)^2=\left(y+z-2x\right)^2+\left(z+x-2y\right)^2+\left(y+z-2z\right)^2\)
⇔ \(y^2-2yz+z^2+z^2-2xz+x^2+x^2-2xy+y^2=\)\(6(z^2-yz-xz+y^2-xy+x^2)\)
⇔ \(2\left(x^2+y^2+z^2-yz-xz-xy\right)\)=\(6(z^2-yz-xz+y^2-xy+x^2)\)
⇔ \(x^2+y^2+z^2-yz-xz-xy\) = \(3(z^2-yz-xz+y^2-xy+x^2)\)
⇔ \(2x^2+2y^2+2z^2-2xy-2xz-2yz=0\)
⇔ \(\left(x-y\right)^2+\left(y-z\right)^2+\left(x-z\right)^2=0\)
Mà \(\left(x-y\right)^2+\left(y-z\right)^2+\left(x-z\right)^2\ge0\forall x;y;z\)
Do đó \(\left\{{}\begin{matrix}x=y\\y=z\\z=x\end{matrix}\right.\)
⇒ \(x=y=z\)
j lắm thế :)))
Bài 2 : ~ bài 1 ngán quá =)))
a, Có
\(5x^2+10y^2-6xy-4x-2y+3\)
\(=\left(x^2-6xy+9y^2\right)+\left(4x^2-4x+1\right)+\left(y^2-2y+1\right)+1\)
\(=\left(x-3y\right)^2+\left(2x-1\right)^2+\left(y-1\right)^2+1>0\forall x;y\)
Do đó không tồn tại x , y tm \(5x^2+10y^2-6xy-4x-2y+3=0\)
b, \(x^2+4y^2+z^2-2x-6x+6y+15=0\)
Câu này đề sai :v bài ngta không cho 2 lần x vậy đâu bạn :)))

a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
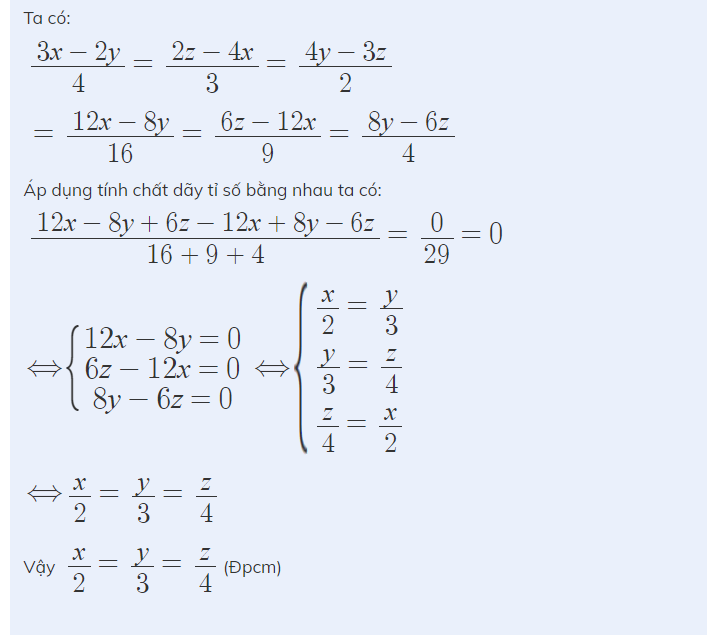
hello bạn chơi minecraft ko
x+y+z=0
=> x2+y2+z2=-2(xy+yz+xz)
=>(x2+y2+z2)2=[-2(xy+yz+xz)]2
<=> x4+y4+z4+2x2y2+2y2z2+2x2z2=4x2y2+4y2z2+4x2z2
=> x4+y4+z4=2(x2y2+y2z2+x2z2)