Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

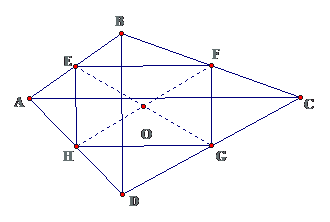
a) A B C D E F G H
Ta nối E và G ; H và F lại với nhau tạo thành hai đường chéo của tứ giác HEFG.
Vì ABCD là hình nhữ nhật nên ABCD là hình thang đặc biệt.
Có: EG là đường trung bình của của hình chữ nhật ABCD ( AE=EB; DG=GC )
=> EG//AD (1)
HF là đường trung bình của hình chữ nhật ABCD ( AH=HD; BF=FC )
=> HF//AB (2)
Theo bài ra: AB _|_ AD ( Tứ giác ABCD là hình chữ nhật )
Từ (1) và (2) suy ra: HF_|_ EG
Tứ giác có hai đường chéo vuông góc với nhau là hình thoi nên HEFG là hình thoi.
Bạn có thể chứng minh theo trục đối xứng.
b) A B C D E F G H I
Gọi I là giao điểm của hai AC và BD (1)
Ta có: AC và BD là hai đường chéo của hình chữ nhật ABCD
=> AI = IC và BI = ID
Xét tam giác ABC có: AE=EB và AI = IC
=> EI là đường trung bình của tam giác ABC
=> EG cắt AC tại I (2)
Xét tam giác ABD có AH=HD và DI=IB
=> HI là đường trung bình của tam giác ABD
=> HF cắt BD tại I (3)
Từ (1),(2),(3) suy ra EG cắt HF tại I (4)
Từ (1),(2),(3),(4) suy ra EG,HF,AC,BD đồng quy tại I

a. Ta có
b. Có là hình bình hành ( dấu hiệu nhận biết )
Mặt khác là hình chữ nhật