Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

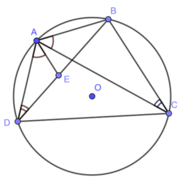
Ta có: `hat(ABD) = hat(ACD)`.
Lấy `M in AC` sao cho `hat(ADB) = hat(MDC)`.
`=> triangle ABD ~ triangle MCD`.
`=> (AB)/(MC) = (BD)/(CD) => AB . CD = BD . MC`.
Xét `2 triangle ADM, BDC`, ta có:
`hat(ADM) = hat(BDC)`.
`(DA)/(DM) = (BD)/(DC) ( triangle ABD ~ triangle MCD )`.
`=> triangle ADM ~ triangle BCD => (AD)/(AM) = (BD)/(CB) => AD . BC = BD . AM`
`=> AD . BC + AD . BC = BD . AM + BD . MC`
`=> AD . BC + AD . BC = BD(AM+MC)`
`=> AD.BC+AD.BC = BD . AC => dpcm`.

vì tứ giác ABCD nội tiếp,theo định lý Ptoleme ta có:
AC.BD=AB.CD+AD.BC (ĐPCM)

Bài 4: Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Các đường cao BD và CE của tam giác ABC cắt nhau tại H (D thuộc AC, E thuộc AB).
a) Chứng minh BCDE là tứ giác nội tiếp
b) Đường thẳng OA cắt đường tròn (O) tại điểm thứ hai là M. Chứng minh BM = CH
c) Giả sử , AB = x. Tính diện tích hình viên phân giới hạn bởi dây AB và cung nhỏ AB theo a và x.

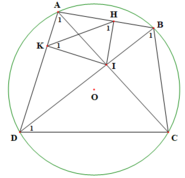
a) Tứ giác AHIK có:
A H I ^ = 90 0 ( I H ⊥ A B ) A K I ^ = 90 0 ( I K ⊥ A D ) ⇒ A H I ^ + A K I ^ = 180 0
=> Tứ giác AHIK nội tiếp.
b) ∆ IAD và ∆ IBC có:
A ^ 1 = B ^ 1 (2 góc nội tiếp cùng chắn cung DC của (O))
A I D ^ = B I C ^ (2 góc đối đỉnh)
=> ∆ IAD ~ ∆ IBC (g.g)
⇒ I A I B = I D I C ⇒ I A . I C = I B . I D
c, Xét đường tròn ngoại tiếp tứ giác AHIK có K ^ 1 = D ^ 1
A ^ 1 = H ^ 1 (2 góc nội tiếp cùng chắn cung IK)
mà A ^ 1 = B ^ 1 ⇒ H ^ 1 = B ^ 1
Chứng minh tương tự, ta được K ^ 1 = D ^ 1
∆ HIK và ∆ BCD có: H ^ 1 = B ^ 1 ; K ^ 1 = D ^ 1
=> ∆ HIK ~ ∆ BCD (g.g)
d) Gọi S1 là diện tích của ∆ BCD.
Vì ∆ HIK ~ ∆ BCD nên:
S ' S 1 = H K 2 B D 2 = H K 2 ( I B + I D ) 2 ≤ H K 2 4 I B . I D = H K 2 4 I A . I C (1)
Vẽ A E ⊥ B D , C F ⊥ B D ⇒ A E / / C F ⇒ C F A E = I C I A
∆ ABD và ∆ BCD có chung cạnh đáy BD nên:
S 1 S = C F A E ⇒ S 1 S = I C I A (2)
Từ (1) và (2) suy ra
S ' S 1 ⋅ S 1 S ≤ H K 2 4 I A . I C ⋅ I C I A ⇔ S ' S ≤ H K 2 4 I A 2 (đpcm)