Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ thấy AB=BC=CD=DE
và \(ABC\ge CDE=>AC\ge CE\)
Tam giác ACE có \(AC\ge CE=>AEC\ge CAE\left(1\right)\)
\(ABC\ge CDE=>\frac{180^0-B}{2}\le\frac{180^0-D}{2}=>BAC\le CED=>CED\ge BAC\left(2\right)\)
Cộng theo vế (1) và (2)
\(AEC+CED\ge CAE+BAC=>E\ge A,mà.E\le A=>E=A\)
Vậy \(A=B=C=D=E\),mà ngũ giác ABCDE có các cạnh = nhau nên là ngũ giác đều

trên tia đối của tia BA lấy điểm B' sao cho góc BB'C=gócADC
tam giác AB'C có :BAC+AB'C+ACB'=180 độ
tam giác ACD có:DAC+D+ACD=180 độ
=>ACB'=ACD
xét tam giác AB'C và tam giác ADC có
B'AC=DAC
AC là cạnh chung
ACB'=ACD
do đó tam giác AB'C= tam giác ADC(g-c-g)
=>DC=B'C(2 cạnh tương ứng)(1)
ta có ABC+D=180 độ (gt)
ABC+B'BC=180 độ(kề bù)
=>góc D=B'BC
mà góc AB'C=D(tam giác AB'C=tam giác ADC)
=>góc B'BC=AB'C(= góc D)
=>tam giác BB'C cân tại C
=>BC=B'C(2)
từ (1) và (2) suy ra :
BC=DC( dpcm)
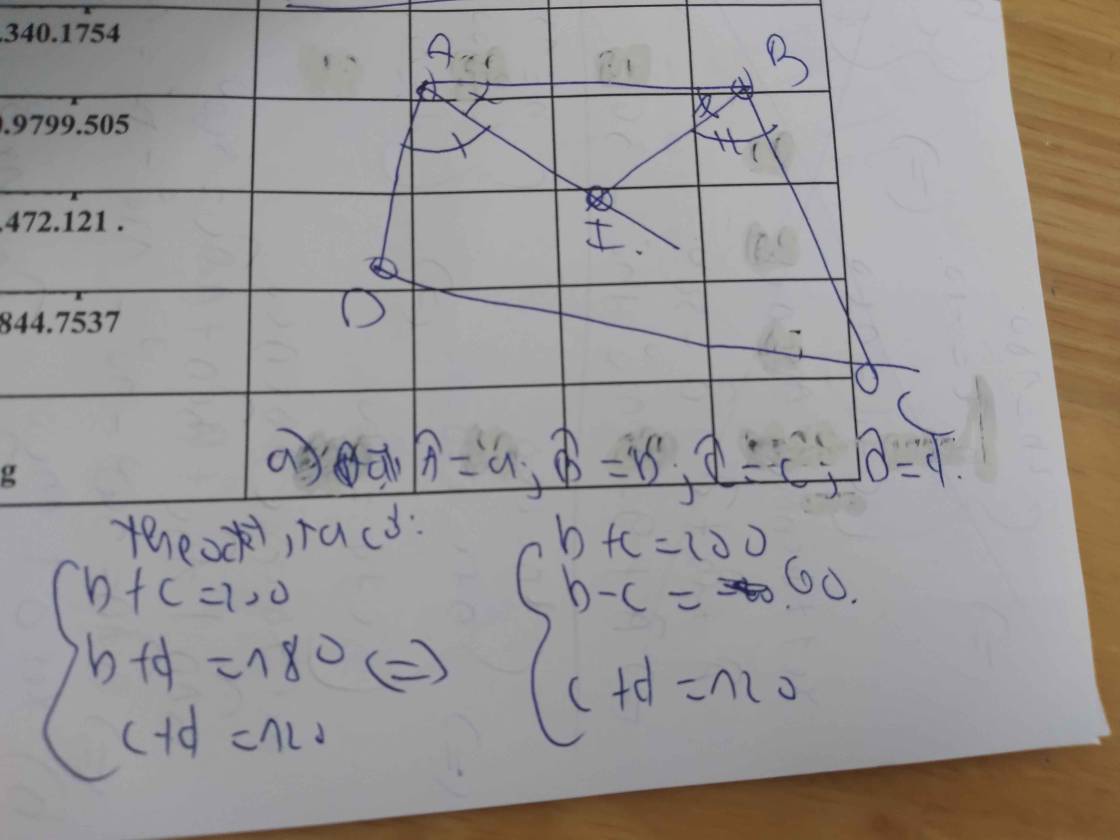

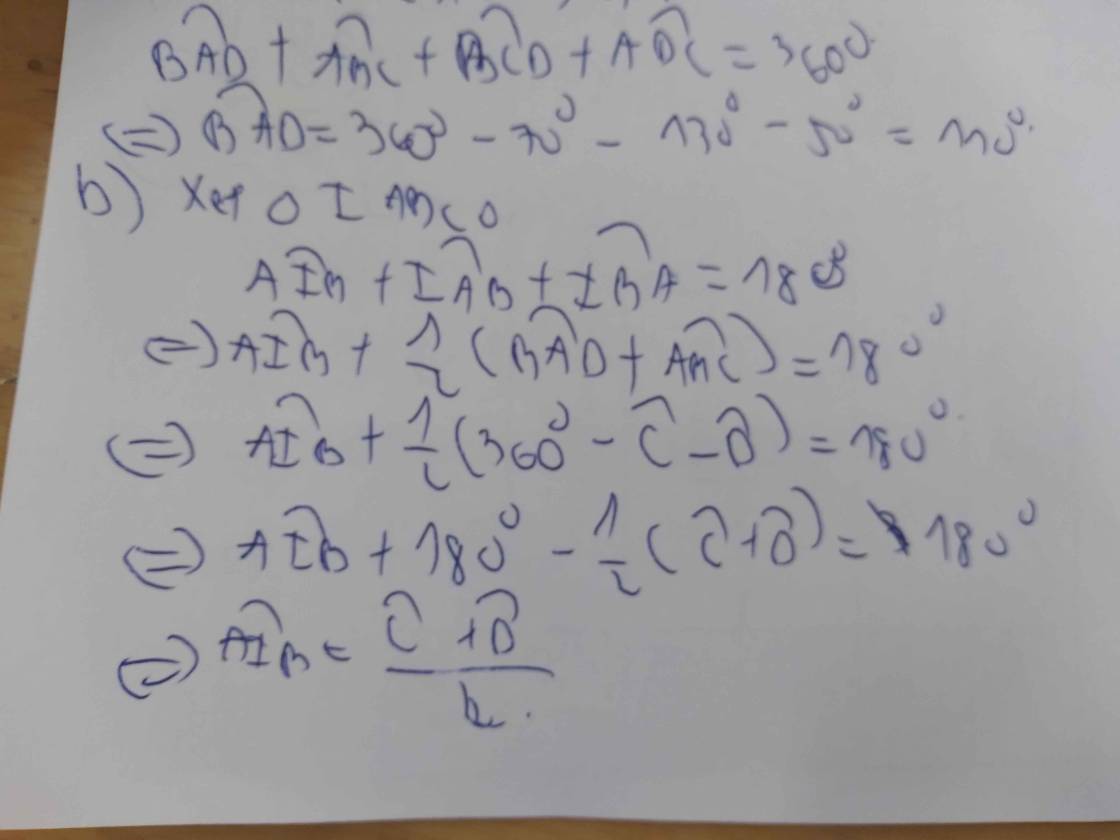
a) Từ GT ta có:
\(\left\{{}\begin{matrix}B+C=200^o\\B+D=180^o\\C+D=120^o\end{matrix}\right.\)
Lấy (1) - (2) ta được:
\(\left\{{}\begin{matrix}C-D=20^o\\C+D=120^o\end{matrix}\right.\)
Giải hệ pt ta được: C = 70o, B = 130o, D = 50o, A = 110o.
b) Có 2 cách để làm:
C1: Thay số đo vào r tính ra ngay:
Khi đó thì góc AIB = 180o - \(\dfrac{1}{2}\)(A + B) = 60o = \(\dfrac{1}{2}\)(C + D).
C2: Ta có:
A + B + C + D = 360o
⇔ C + D = 360o - 2.\(\dfrac{1}{2}\)(A + B) = 360o - 2.(180o - AIB) = 2.AIB
⇔ \(\dfrac{1}{2}\)(C + D) = AIB (đpcm)