Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét tam giác AOB và tam giác DOC có:
góc AOB= góc COD
góc ABD=góc ACD
do đó : tam giác AOB đồng dạng với tam giác DOC(g-g)
b, theo cm câu a: tam giác AOB đồng dạng với tam giác DOC
=> \(\frac{AO}{OD}=\frac{OB}{OC}\)
xét tam giác AOD và tam giác BOC có:
\(\frac{OA}{OD}=\frac{OB}{OC}\)
góc AOD= góc BOC(2 góc đối đỉnh)
do đó: tam giác AOD đồng dạng với tam giác BOC(c-g-c)
c, xét tam giác DBE và tam giác CAE có:
góc DEC chung
góc EDB=góc ACE( 2 góc tương ứng của tam giác AOD đồng dạng với tam giác BOC)
do đó: tam giác DBE đồng dạng với tam giác CAE(g-g)
=>\(\frac{EB}{EA}=\frac{ED}{EC}\)
\(\Rightarrow EA.ED=EB.EC\)

Làm cả 3 phần :))
Giải
a) Xét △AOB và △DOC có :
góc ABD = góc ACD ( gt )
góc AOB = góc DOC ( đđ )
=> ΔAOB đồng dạng ΔDOC (g.g ) (đpcm)
b) Xét ΔAOD và ΔBOC có :
góc AOD = góc BOC ( đđ )
OBOA=OCODOBOA=OCOD ( ΔAOB đồng dạng ΔDOC)
=> ΔAOD đồng dạng ΔBOC ( c.g.c ) ( đpcm )
c) Xét ΔAEC và ΔBED có :
góc E chung
gócADO = góc BCO ( ΔAOD đồng dạng ΔBOC )
=> ΔAEC đồng dạng ΔBED ( g.g )
=> EAEB=ECEDEAEB=ECED => EA.ED=EB.EC (đpcm)

Xét △ AOB và △ DOC, ta có:
∠ (ABD) = ∠ (ACD) (gt)
Hay ∠ (ABO) = ∠ (OCD)
∠ (AOB) = ∠ (DOC) (đối đỉnh)
Vậy △ AOB đồng dạng △ DOC (g.g)
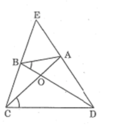
Thật ra thì bạn chỉ cần vẽ một đường tròn bất kì, xong lấy bốn điểm A,B,C,D trên đườg tròn đó là xong
a: Xét ΔAOB và ΔDOC có
góc AOB=góc DOC
góc ABO=góc DCO
Do đó: ΔAOB đồng dạng với ΔDOC
b: Ta có: ΔAOB đồng dạng với ΔDOC
nên OA/OD=OB/OC
=>OA/OB=OD/OC
Xét ΔOAD và ΔOBC có
OA/OB=OD/OC
góc AOD=góc BOC
Do đo: ΔOAD đồng dạng với ΔOBC
c: Xét ΔEAB và ECD có
góc EAB=góc ECD
góc AEB chung
Do đó; ΔEAB đồg dạng với ΔECD
Suy ra: EA/EC=EB/ED
hay \(EA\cdot ED=EB\cdot EC\)