Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có MNPQ là hình chữ nhật tâm O => M,N,P,Q cùng thuộc (O;OM)
A B C D I E O
Cô hướng dẫn nhé. :)
Tứ giác AIDE nội tiếp đường tròn đường kính AI.
b. Do câu a ta có AIDE là tứ giác nội tiếp nên gó IDE = góc IAE. Lại có góc IAE = góc CDB. Từ đó suy ra DB là tia phân giac góc CDE.
c. Ta thấy góc CDE = 2 góc CAB (Chứng minh b). Lại có góc COB = 2 góc CAB. Từ đó suy ra góc CDE = góc COB. Hay OEDC là tứ giác nội tiếp ( Góc ngoài ở đỉnh bằng góc đối diện )
Chúc em học tốt ^^
Em tham khảo link dưới
chứng minh MNPQ là hình chữ nhật
=> M, N, P, Q cùng nằm trên một đường tròn.
Câu hỏi của Nàng tiên cá - Toán lớp 8 - Học toán với OnlineMath
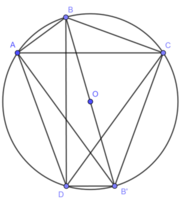
Kẻ đường kính BB’. Nối B’A, B’D, B’C.
Ta có: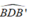
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ AC // B'D ( cùng vuông góc với BD)
Suy ra, tứ giác ADB’C là hình thang
Vì ADB’C nội tiếp đường tròn (O) nên ADB’C là hình thang cân
⇒ CD = AB'
⇒ A B 2 + C D 2 = A B 2 + A B ' 2
Mà tam giác BAB’ vuông tại A do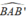 
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ A B 2 + C D 2 = A B 2 + A B ' 2 = 2 R 2 = 4 R 2 (đpcm)
A B D C H
a/ Xét tam giác AHD và tam giác BCH có:
góc AHD = góc BHC = 90 độ (gt)
góc DAH = góc DBC (hai góc = nhau cùng nhìn cạnh DC, tứ giác ABCD nội tiếp)
=> tam giác AHD đồng dạng tam giác BHC (g.g)
=> HA/HB = HD/HC
=> HA.HC = HB.HD