Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi
#Hỏi cộng đồng OLM
#Toán lớp 10
Ta chứng minh hai mệnh đề:
– Khi =
thì ABCD là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
=
⇔
=
và và
cùng hướng.
và
cùng hướng =>
và
cùng phương, suy ra giá của chúng song song với nhau, hay AB // DC (1)
Ta lại có =
=> AB = DC (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác ABCD có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
– Khi ABCD là hình bình hành thì =
Khi ABCD là hình bình hành thì AB // CD. Dễ thấy, từ đây ta suy ra hai vec tơ và
cùng hướng (3)
Mặt khác AB = CD => =
(4)
Từ (3) và (4) suy ra =
.
bạn cho mình hỏi: nếu vecto AB = vecto AB thì làm sao cùng hướng được, có thể ngược hướng mà
Cho hình bình hành ABCD. Chứng minh rằng:
#Hỏi cộng đồng OLM
#Toán lớp 10
Cho tam giác ABC cạnh a. Tính độ dài của các vectơ
#Hỏi cộng đồng OLM
#Toán lớp 10
Ta có +
=
=
= a
Ta có: –
=
+
.
Trên tia CB, ta dựng =
=> –
=
+
=
Tam giác EAC vuông tại A và có : AC = a, CE = 2a , suy ra AE = a√3
Vậy =
= a√3
Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng
#Hỏi cộng đồng OLM
#Toán lớp 10
Ta xét tổng:
+
+
+
+
+
=
=
(1)
Mặt khác, ta có ABIJ, BCPQ và CARS là các hình bình hành nên:
=
=
=
=> +
+
=
+
+
=
=
(2)
Từ (1) và (2) suy ra : +
+
=
(dpcm)
Cho hình bình hành ABCD và một điểm M tùy ý. Chứng minh rằng
#Hỏi cộng đồng OLM
#Toán lớp 10
Áp dụng quy tắc 3 điểm đối với phép cộng vectơ:
=
+
=
+
=> +
=
+
+ (
+
)
ABCD là hình bình hành, hi vec tơ và
là hai vec tơ đối nhau nên:
+
=
Suy ra +
=
+
.
Mình có cách khác :
Áp dụng quy tắc 3 điểm đối với phép trừ vec tơ
=
–
=
–
=> +
= (
+
) – (
+
).
ABCD là hình bình hành nên và
là hai vec tơ đối nhau, cho ta:
+
=
Suy ra: +
=
+
.
Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ
#Hỏi cộng đồng OLM
#Toán lớp 10
Gọi G là giao điểm của AK, BM thì G là trọng tâm của tam giác.
Ta có =
=>
=
= –
= –
= –
Theo quy tắc 3 điểm đối với tổng vec tơ:
=
+
=>
=
–
=
(
–
).
AK là trung tuyến thuộc cạnh BC nên
+
= 2
=>
–
+
= 2
Từ đây ta có =
+
=>
= –
–
.
BM là trung tuyến thuộc đỉnh B nên
+
= 2
=> –
+
= 2
=> =
+
.
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy một điểm M sao cho
#Hỏi cộng đồng OLM
#Toán lớp 10
Trước hết ta có
= 3
=>
= 3 (
+
)
=> = 3
+ 3
=> – = 3
=> =
mà =
–
nên
=
(
–
)
Theo quy tắc 3 điểm, ta có
=
+
=>
=
+
–
=> = –
+
hay
= –
+
– Khi
= 
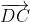thì ABCD là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
và
và 
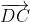cùng hướng.
Ta lại có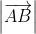
= 
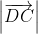=> AB = DC (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác ABCD có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
– Khi ABCD là hình bình hành thì
= 
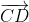
Khi ABCD là hình bình hành thì AB // CD. Dễ thấy, từ đây ta suy ra hai vec tơ
và 
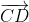cùng hướng (3)
Mặt khác AB = CD =>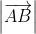
= 
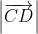(4)
Từ (3) và (4) suy ra
= 
.
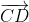Ta có Vecto AB= Vecto DC
\(\Rightarrow AB=DC\)
\(\Rightarrow\)Vecto AB,DC cùng phương
\(\Rightarrow\)AB trùng DC hoặc AB song song DC
mà ABCD là tứ giác
\(\Rightarrow\)ABCD là hình bình hành