Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

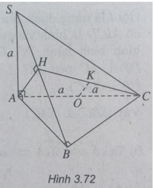
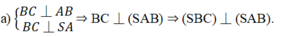
b) AH ⊥ SB mà SB là giao tuyến của hai mặt phẳng vuông góc là (SBC) và (SAB) nên AH ⊥ (SBC).
c) Xét tam giác vuông SAB với đường cao AH ta có:
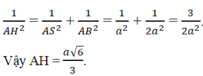
d) Vì OK ⊥ (SBC) mà AH ⊥ (SBC) nên OK // AH, ta có K thuộc CH.
OK = AH/2 = (a√6)/6.

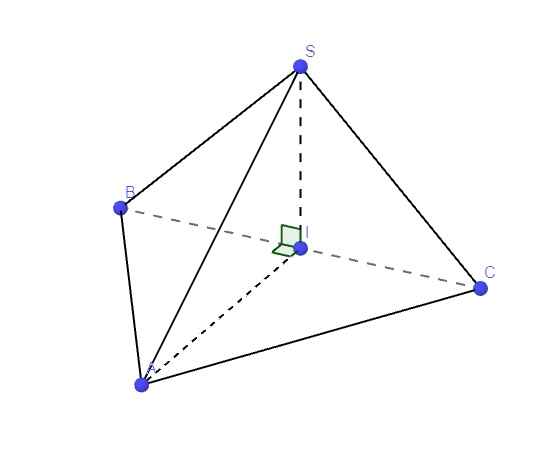
S A B C I H O K
a) \(SB^2=AS^2+AB^2=AS^2+AC^2=SC^2\Rightarrow SB=SC\) => \(\Delta\)SBC cân tại S
Do đó: AO,SH cắt nhau tại trung điểm I của cạnh BC
Xét \(\Delta\)SBC: trực tâm H, đường cao SI => \(IH.IS=IB.IC\)(1)
Tương tự: \(IB.IC=IO.IA\)(2)
Từ (1);(2) => \(IH.IS=IO.IA\)=> \(\Delta\)IHO ~ \(\Delta\)IAS => ^IHO = ^IAS = 900 => OH vuông góc IS (3)
Ta có: BC vuông góc với AI,AS => BC vuông góc với (SAI) => BC vuông góc OH (4)
Từ (3);(4) => OH vuông góc (SBC).
b) Xét tam giác SKI: IO vuông góc SK tại A, KO vuông góc SI tại H (cmt) => O là trực tâm tam giác SKI
Vậy SO vuông góc IK.

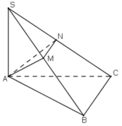
a.
Do ABC đều \(\Rightarrow\) AI là trung tuyến đồng thời là đường cao
\(\Rightarrow AI\perp BC\) (1)
SBC vuông cân tại S \(\Rightarrow SI\) là trung tuyến kiêm đường cao
\(\Rightarrow SI\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAI\right)\Rightarrow BC\perp SA\)
b.
\(SA>AI\Rightarrow\widehat{SIA}>\widehat{ASI}\Rightarrow\widehat{ASI}\) là góc nhọn
Do ABC đều \(\Rightarrow AI=\dfrac{a\sqrt{3}}{2}\)
SBC vuông cân tại S \(\Rightarrow SI=\dfrac{1}{2}BC=\dfrac{a}{2}\)
Áp dụng định lý hàm sin cho tam giác SAI:
\(\dfrac{SI}{sin\widehat{IAS}}=\dfrac{AI}{sin\widehat{ASI}}\Rightarrow sin\widehat{ASI}=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{ASI}=60^0\) (do \(\widehat{ASI}\) nhọn)
\(\Rightarrow=180^0-\left(30^0+60^0\right)=90^0\)
Hay \(SI\perp IA\)



Biết SA và DA làm sao nhỉ? Đề bị lỗi