Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
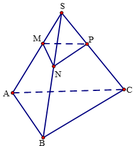
Gọi N, P là hai điểm lần lượt thuộc S B , S C thỏa mãn M N / / A B , M P / / A C .
Ta có M N // A B ⇒ M N // A B C M P // A C ⇒ M P // A B C ⇒ M N P / / A B C .
Gọi h 1 là đường cao của ΔMNP ứng với đáy MN.
Gọi h 2 là đường cao của ΔABC ứng với đáy AB.
Dễ thầy ΔMNP đồng dạng ΔABC ta có M N A B = h 1 h 2 = k .
Vậy để thỏa mãn yêu cầu bài toán
S Δ M N P S Δ A B C = 1 2 h 1 . M N 1 2 h 2 . A B = 1 2 ⇔ k . k = 1 2 ⇔ k = 2 2

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2







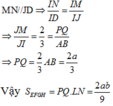



Đáp án B.
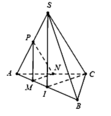
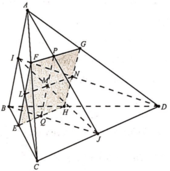
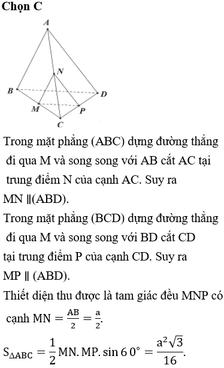
Trong A B C kẻ M P / / C I P ∈ A C . Trong S A C kẻ P N / / S C N ∈ S A .
⇒ M N P / / S I C ⇒ M N P ≡ α
Suy ra thiết diện giữa α và tứ diện S.ABC là tam giác MNP.
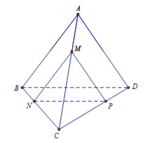
Do S.ABC là tứ diện đều nên ta đặt S A = S B = S C = S D = A B = B C = C A = 2 x
⇒ A I = x ; C I = 2 x 3 2 = x 3
Ta có M P / / C I ⇒ M P C I = A P A C = A M A I = a x ⇒ M P = a x . x 3 = a 3
Tương tự ta có M N = a 3 .
Ta có N P S C = A P A C = a x ⇒ N P = a x . S C = a x .2 x = 2 a .
Chu vi tam giác MNP là C = 2 a + a 3 + a 3 = 2 a 1 + 3 . Ta chọn B.