Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
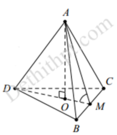
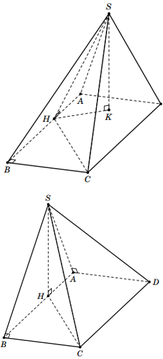
Gọi M là trung điểm của
B C ⇒ A M ⊥ B C D M ⊥ B C ⇒ B C ⊥ A D M
Suy ra
A B C ; D B C ^ = A M ; D M ^ = A D M ^ = φ
Gọi O là hình chiếu của A lên
mặt phẳng B C D
⇒ O là trọng tâm của tam giác BCD
⇒ O M = D M 3 = 1 3 . a 3 2 = a 3 6
Tam giác AMO vuông tại O, có
cos A M D ^ = O M A M = a 3 6 : a 3 2 = 1 3
Vậy cos φ = 1 3

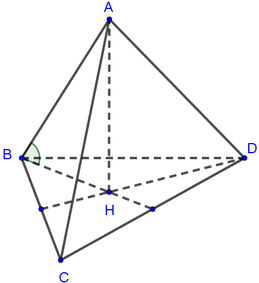
a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

Đáp án B
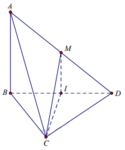
Gọi I là trung điểm BD. Khi đó I C M ^ = φ
Ta có: tan φ = I M C I = a a 3 2 = 2 3 3

a) ∆DEI = ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
=> ∆DEI = ∆DFI (c.c.c)
D E I F
b) Vì ∆DEI = ∆DFI => \(DIE=DIF\)
mà \(DIE+DIF=180^0\) (kè bù)
nên \(DIE=DIF=90^0\)
c) I là trung điểm của EF nên IE = IF = 5cm
∆DEI vuông tại I => DI2 = DE2 – EI2 (định lí pytago)
=> DI2 = 132 – 52 = 144
=> DI = 12
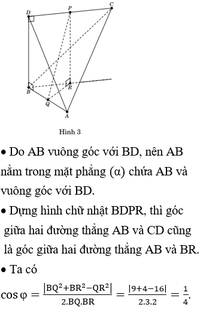

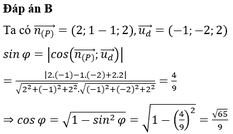





Ta có biến đổi sau: