K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
1 tháng 2 2019
Ta có:
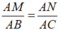
suy ra MN // BC (1) (Định lý Ta-lét đảo).
- Lại có: MN ∩ (MNI) (2)
- Từ (1) và (2) suy ra: BC // (MNI)

CM
7 tháng 2 2019
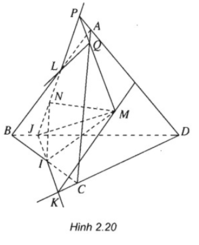
a) Nhận xét:
Do giả thiết cho IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K = IJ ∩ CD.
Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);
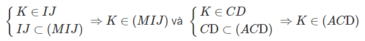
Vậy (MIJ) ∩ (ACD) = MK
b) Với L = JN ∩ AB ta có:
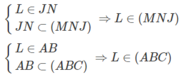
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P = JL ∩ AD, Q = PM ∩ AC
Ta có:
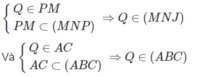
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ = (ABC) ∩ (MNJ).

12 tháng 8 2021
Trong (ABC) gọi K là giao điểm của MN và BC
Trong (BCD) gọi E và F là giao điểm của IK với CD và BD
=> Thiết diện là tứ giác MNEF
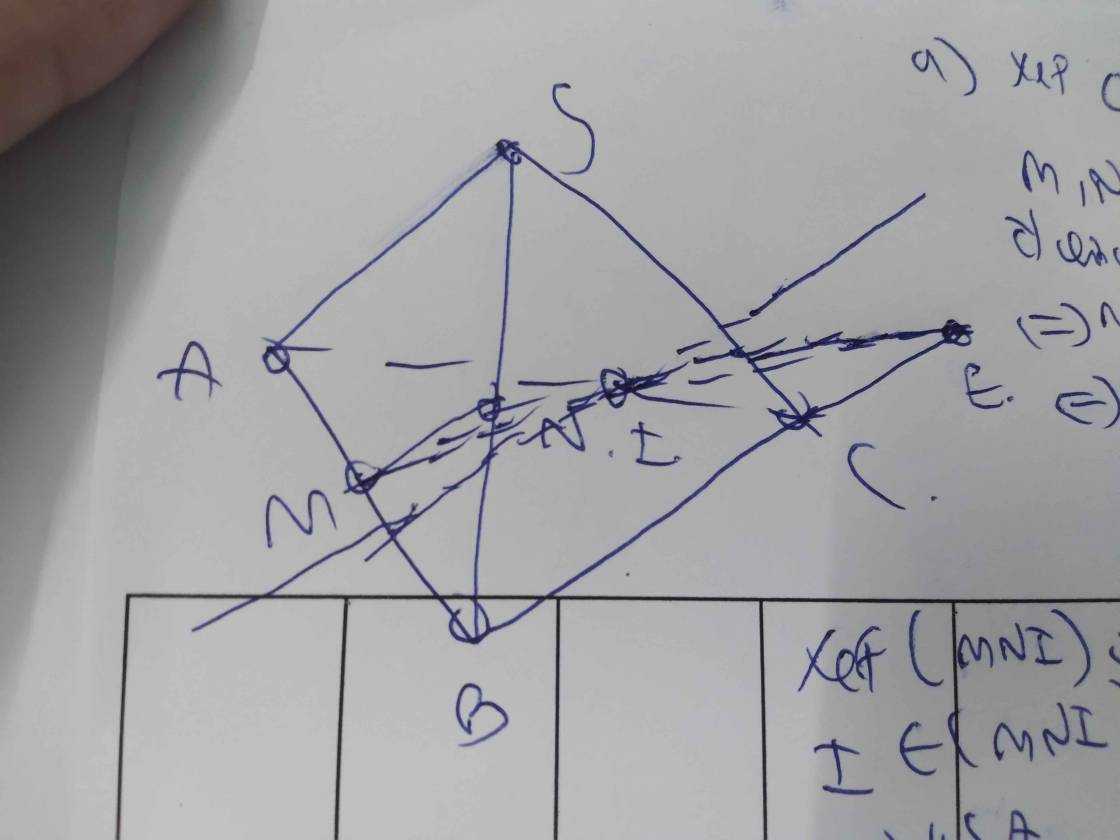


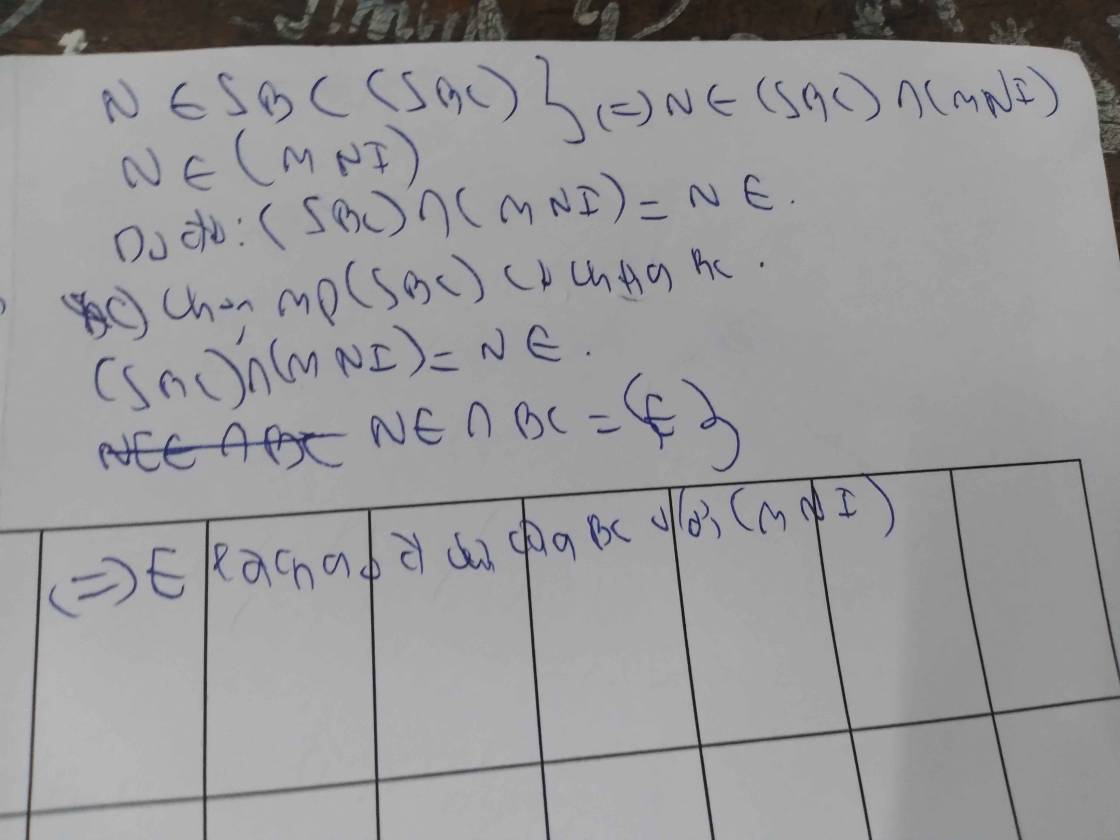
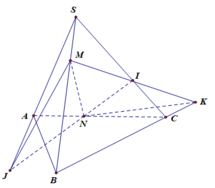



a/ MN là giao tuyến của (MNI) và (ABC)
b/ MI là giao tuyến của (MNI) và (ABD)
c/ Kéo dài MN cắt BC tại P, nối PI kéo dài cắt CD tại Q
\(\Rightarrow IQ\) là giao tuyến của (MNI) và (BCD)
d/ NQ là giao tuyến của (MNI) và (ACD)