K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

15 tháng 11 2023
Gọi N là trung điểm của BC
Xét ΔABC có
N,P lần lượt là trung điểm của BC,BA
=>NP là đường trung bình của ΔABC
=>NP//AC
=>Hình chiếu song song của điểm P theo phương AC lên mp(BCD) là điểm N

NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2020
Gọi H là hình chiếu vuông góc của A lên (BCD)
\(AB=AC=AD\Rightarrow HA=HB=HC\Rightarrow H\) là tâm đáy
\(\Rightarrow DH\perp BC\)
Mà \(AH\perp\left(BCD\right)\Rightarrow AH\perp BC\)
\(\Rightarrow BC\perp\left(ADH\right)\Rightarrow BC\perp AD\)
b/ Chắc bạn nhầm đề?
Hoàn toàn tương tự câu a, ta chứng minh được \(CD\perp\left(ABH\right)\Rightarrow CD\perp AB\Rightarrow\left(AB;CD\right)=90^0\)
Điểm I để làm gì nhỉ? :<
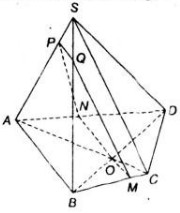

Gọi K là trung điểm của CD
Xét ΔADC có
Q,K lần lượt là trung điểm của DA,DC
=>QK là đường trung bình của ΔADC
=>QK//AC
=>Hình chiếu song song của điểm Q theo phương AC lên mp(BCD) là điểm K