Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong mp(BCD), gọi E là giao điểm của JK và CD
Ta có: \(IE\cap AD=\left\{F\right\}\)
\(IE\subset\left(IJK\right)\)
Do đó: \(AD\cap\left(IJK\right)=F\)
Xét ΔACD có I,F,E thẳng hàng
nên \(\dfrac{AI}{IC}\cdot\dfrac{CE}{ED}\cdot\dfrac{DF}{FA}=1\)
=>\(1\cdot2\cdot\dfrac{DF}{FA}=1\)
=>\(\dfrac{FD}{FA}=\dfrac{1}{2}\)
=>\(\dfrac{FA}{FD}=2\)

I, J lần lượt là trung điểm của AC và BC nên IJ // AB. Do đó giao tuyến của (IJK) với (ABD) là đường thẳng đi qua K và song song với AB cắt AD tại H. Vậy IJ // KH // AB. Ta có ∆BJK = ∆AIH ⇒ JK = IH. Hơn nữa KH ≠ IJ.
Vậy thiết diện là hình thang cân IJKH
Đáp án A

a) Xét (IJK) và (ACD)
có I thuộc (IJK) giao (ACD)
Trong (BCD) vẽ JK cắt CD tại E
=> E thuộc (IJK) giao (ACD) (đoạn này m ghi tắt :D)
Vậy IE là giao tuyến của (IJK) và (ACD)
Ta có E thuộc IE, IE là con của (IJK)
E thuộc CD
=> E là giao điểm của CD với (IJK)
b) Xét (ABD) và (IJK)
K thuộc (ABD) giao (IJK)
=> Kx là giao tuyến của (ABD) và (IJK)
mà AB // IJ
=> Kx // AB
Trong (ABD) vẽ Kx cắt AD tại F
=> F là giao điểm của AD và (IJK)
Ta có Kx // AB và Kx // IJ (cmt)
mà F thuộc Kx
=> KF // IJ

Trong mp (ACD) kéo dài MN và CD cắt nhau tại I
Trong mp (BCD) nối IQ cắt BD tại J
Áp dụng định lý Menelaus trong tam giác ACD:
\(\dfrac{AM}{MC}.\dfrac{CI}{ID}.\dfrac{DN}{NA}=1\Rightarrow1.\dfrac{CI}{ID}.\dfrac{1}{2}=1\Rightarrow IC=2ID\)
Do \(BC=4BQ\Rightarrow QC+QB=4QB\Rightarrow QC=3QB\)
Menelaus cho tam giác BCD:
\(\dfrac{QC}{QB}.\dfrac{BJ}{JD}.\dfrac{DI}{IC}=1\Rightarrow3.\dfrac{BJ}{JD}.\dfrac{1}{2}=1\Rightarrow\dfrac{BJ}{JD}=\dfrac{2}{3}\)
Menelaus cho tam giác CQI:
\(\dfrac{ID}{DC}.\dfrac{CB}{BQ}.\dfrac{QJ}{JI}=1\Rightarrow1.4.\dfrac{JQ}{JI}=1\Rightarrow\dfrac{JQ}{JI}=\dfrac{1}{4}\)
\(\Rightarrow\dfrac{JB}{JD}+\dfrac{JQ}{JI}=\dfrac{2}{3}+\dfrac{1}{4}=\dfrac{11}{12}\)

Đáp án C.
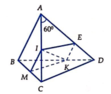
+ (ABD) và (IMK) có điểm chung là k và lần lượt chứa hai đường thẳng AB // MI
=> Giao tuyến của (ABD) và (IMK) là đường thẳng đi qua K và song song với AB và AD tại E Thiết diện cần tìm là tứ giác MKEI có
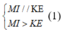
![]()
Từ (1) và (2) => Tứ giác MKEI là hình thang cân với đáy lớn là MI

+ Có
![]()
![]()
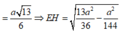
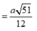
![]()
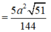
Gọi H là hình chiếu vuông góc của E lên MI 2IH + EK = IM

Trong mp (ACD), kéo dài IJ cắt CD tại E thì E là giao điểm của CD và (IJK)

Em coi lại đề, M là trung điểm của AC và BC? 1 điểm làm sao là trung điểm của 2 đoạn này được nhỉ?
M là trung điểm của AC và BD đúng ko nhỉ