Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
s B A D C O M
Hình chiếu vuông góc của SA lên (ABCD) là AO nên góc giữa SA và (ABCD) là \(\widehat{SAO}\)
Xét \(\Delta SAO\left(\perp O\right)\) ta có : \(SA=\frac{a\sqrt{5}}{2};AO=\frac{1}{2}AC=\frac{1}{2}a\sqrt{2}\)
\(\cos\widehat{SAO}=\frac{AO}{SA}=\frac{\frac{a\sqrt{2}}{2}}{\frac{a\sqrt{5}}{2}}=\frac{\sqrt{10}}{5}\)
c. Xét \(\Delta SOC\) có : \(\begin{cases}SO\perp BD\\OC\perp BD\end{cases}\) nên \(\left(SOC\right)\perp BD\) mà \(OM\subset\left(SOC\right)\Rightarrow OM\perp BD\)
xét : \(\left(MBD\right)\cap\left(ABCD\right)=BD\)
Trong (MBD) có \(OM\perp BD\)
Trong (ABCD) có \(OC\perp BD\)
Vậy góc giữa (MBD) và (ABCD) là \(\widehat{MOC}\)
Ta có : \(\Delta SAC\) đồng dạng với \(\Delta MOC\) (vì \(CM=\frac{1}{2}CS;CO=\frac{1}{2}CA\))nên \(\widehat{MOC}=\widehat{SAC}\)
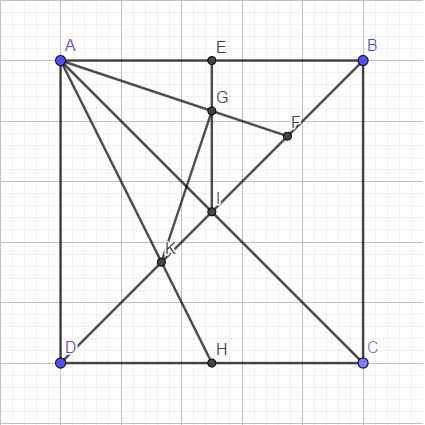
Đặt tên điểm như hình vẽ bên dưới
Ta có: F là trung điểm BI \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AF}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)=\dfrac{1}{3}\left(\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\)
\(\overrightarrow{AH}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AK}=\dfrac{2}{3}\overrightarrow{AH}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}\)
\(\overrightarrow{GK}=\overrightarrow{GA}+\overrightarrow{AK}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{6}\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}=-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AG}.\overrightarrow{GK}=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)=-\dfrac{1}{12}AB^2+\dfrac{1}{12}AD^2=0\)
\(\Rightarrow AG\perp GK\)
\(\left\{{}\begin{matrix}\overrightarrow{GA}=\left(a+\dfrac{1}{3};b\right)\\\overrightarrow{KG}=\left(0;\dfrac{5}{3}\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{GA}.\overrightarrow{KG}=\left(a+\dfrac{1}{3}\right).0+\dfrac{5}{3}b=0\Rightarrow b=0\)
Mặt khác: \(AG^2-GK^2=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)^2-\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)^2=0\)
\(\Rightarrow AG^2=GK^2\Rightarrow\left(a+\dfrac{1}{3}\right)^2=\left(\dfrac{5}{3}\right)^2\Rightarrow a=-2\)
A B C D M N P I K K X Y Z
a/
Ta có
M là trọng tâm tg ABC \(\Rightarrow\dfrac{MI}{MA}=\dfrac{1}{2}\)
N là trọng tâm tg ACD \(\Rightarrow\dfrac{NK}{NA}=\dfrac{1}{2}\)
Xét tg AIK có
\(\dfrac{MI}{MA}=\dfrac{NK}{NA}=\dfrac{1}{2}\) => MN//IK (Talet đảo trong tam giác)
Ta có
\(I\in BC;BC\in\left(BCD\right)\Rightarrow I\in\left(BCD\right)\)
\(K\in CD;CD\in\left(BCD\right)\Rightarrow K\in\left(BCD\right)\)
\(\Rightarrow IK\in\left(BCD\right)\) Mà MN//IK (cmt) => MN//(BCD)
Các trường hợp khác c/m tương tự
b/
Trong (ABC) từ M dưng đường thẳng // BC cắt AB; AC tại X và Y
Trong (ACD) nối YN cắt AD tại Z
Xét tg ABC có
\(\dfrac{XB}{XA}=\dfrac{YC}{YA}=\dfrac{MI}{MA}=\dfrac{1}{2}\) (Talet trong tam giác)
XY//BC; \(BC\in\left(BCD\right)\) => XY//(BCD)
Xét tg ACK có
\(\dfrac{YC}{YA}=\dfrac{NK}{NA}=\dfrac{1}{2}\) => YN//CK => YZ//CD
mà \(CD\in\left(BCD\right)\) => YZ//(BCD)
=> (XYZ)//(BCD)
Ta có MP//(BCD); MN//(BCD) => (MNP)//(BCD)
mà \(M\in\left(MNP\right);M\in\left(XYZ\right)\)
\(\Rightarrow\left(MNP\right)\equiv\left(XYZ\right)\) (Từ 1 điểm ngoài 1 mặt phẳng cho trước chỉ có duy nhất 1 mặt phẳng đi qua điểm đã cho và // với mặt phẳng cho trước)
=> (XYZ) là thiết diện của tứ diện ABCD khi cắt bởi (MNP)
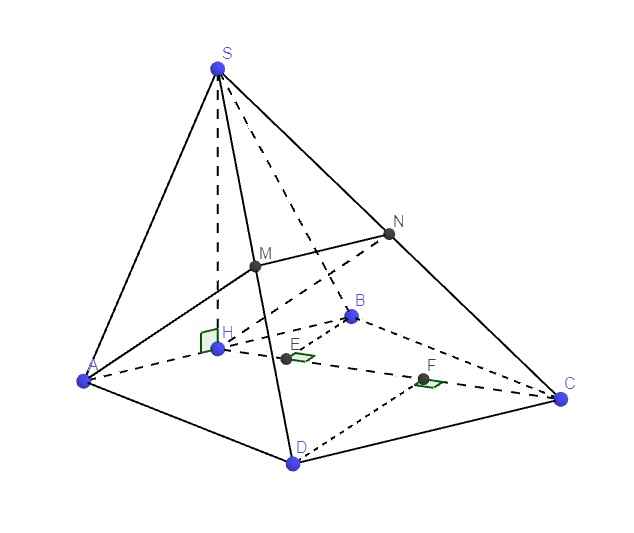
S A B C D H M N O
Cần câu d thôi đúng ko bạn?
\(ID\) cắt (SAC) tại A mà \(IA=2DA\Rightarrow d\left(I;\left(SAC\right)\right)=2d\left(D;\left(SAC\right)\right)\)
\(BD\) cắt (SAC) tại O mà \(OB=OD\Rightarrow d\left(D;\left(SAC\right)\right)=d\left(B;\left(SAC\right)\right)\)
Mặt khác \(BA=2HA\Rightarrow d\left(B;\left(SAC\right)\right)=2d\left(H;\left(SAC\right)\right)\)
\(\Rightarrow d\left(I;\left(SAC\right)\right)=4d\left(H;\left(SAC\right)\right)\)
Từ H kẻ \(HM\perp AC\), từ H kẻ \(HN\perp SM\Rightarrow HN=d\left(H;\left(SAC\right)\right)\)
Áp dụng hệ thức lượng: (chú ý rằng \(AH=\frac{AB}{2}=\frac{a}{2};OH=\frac{AD}{2}=\frac{a\sqrt{2}}{2}\))
\(\frac{1}{HM^2}=\frac{1}{AH^2}+\frac{1}{OH^2}\Rightarrow HM=\frac{AH.OH}{\sqrt{AH^2+OH^2}}=\frac{a\sqrt{6}}{6}\)
\(\frac{1}{HN^2}=\frac{1}{SH^2}+\frac{1}{HM^2}\Rightarrow HN=\frac{SH.HM}{\sqrt{SH^2+HM^2}}=\frac{a\sqrt{57}}{19}\)
\(\Rightarrow d\left(I;\left(SAC\right)\right)=\frac{4a\sqrt{57}}{19}\)
Tam giác SAB đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}AB=\left(SAB\right)\cap\left(ABCD\right)\\\left(SAB\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Gọi N là trung điểm SC \(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow\left\{{}\begin{matrix}MN||CD\\MN=\dfrac{1}{2}CD\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}MN||AH\\MN=AH\end{matrix}\right.\) \(\Rightarrow AMNH\) là hbh
\(\Rightarrow AM||HN\Rightarrow AM||\left(SHC\right)\)
\(\Rightarrow d\left(AM;SC\right)=d\left(AM;\left(SHC\right)\right)=d\left(A;\left(SHC\right)\right)\)
Mặt khác H là trung điểm AB \(\Rightarrow d\left(A;\left(SHC\right)\right)=d\left(B;\left(SHC\right)\right)\)
Từ B kẻ \(BE\perp HC\Rightarrow BE\perp\left(SHC\right)\) (do \(SH\perp BE\))
\(\Rightarrow BE=d\left(B;\left(SHC\right)\right)\)
Hệ thức lượng: \(BE=\dfrac{BH.BC}{CH}=\dfrac{BH.BC}{\sqrt{BH^2+BC^2}}=\dfrac{a\sqrt{5}}{5}\)
b.
Từ D kẻ \(DF\perp HC\Rightarrow DF\perp\left(SHC\right)\) (do \(SH\perp DF\))
\(\Rightarrow DF=d\left(D;\left(SHC\right)\right)\)
\(DF=DC.cos\widehat{FDC}=DC.cos\widehat{BCH}=\dfrac{DC.BC}{CH}=\dfrac{DC.BC}{\sqrt{BC^2+BH^2}}=\dfrac{2a\sqrt{5}}{5}\)
phần c là hỏi về thiết diện của tứ diện ABCD cắt bởi (AG1G2) đk bn ???🤔
Đáp án A.
Gọi I là tâm mặt cầu ngoại tiếp ABCD => I ∈ ∆ và IA = IB = R
=> Thể tích mặt cầu ngoại tiếp ABCD nhỏ nhất ⇔ IB nhỏ nhất