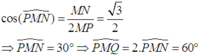
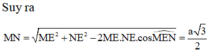
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B và D giống nhau nên chắc chắn cả 2 đều đúng
Kiểm tra 2 đáp án A và C:
\(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{MC}+\overrightarrow{MD}\right)=\frac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{AC}+\overrightarrow{MB}+\overrightarrow{BD}\right)=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{BD}\right)\)
Vậy đáp án A đúng nên đáp án C sai

a: Chọn mp(ACD) có chứa MN
Trong mp(BCD), gọi K là giao điểm của BO và CD
K∈BO⊂(ABO)
K∈CD⊂(ACD)
Do đó: K∈(ABO) giao (ACD)(1)
ta có: A∈(ABO)
A∈(ACD)
Do đó: A∈(ABO) giao (ACD)(2)
Từ (1),(2) suy ra (ABO) giao (ACD)=AK
Gọi H là giao điểm của AK và MN
=>H là giao điểm của MN và (BAO)
b: Chọn mp(ABK) có chứa AO
H∈AK⊂(ABK)
H∈MN⊂(BMN)
Do đó: H∈(ABK) giao (BMN)(3)
Ta có: B∈(ABK)
B∈(BMN)
Do đó: B∈(ABK) giao (BMN)(4)
Từ (3),(4) suy ra (ABK) giao (BMN)=BH
Gọi I là giao điểm của BH và AO
=>I là giao điểm của AO và mp(BMN)

Đáp án C
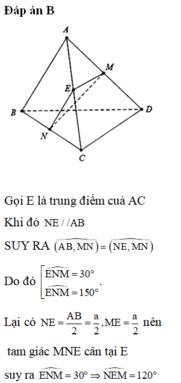
Qua M vẽ đường thẳng song song với AB cắt AC tại P và vẽ đường thẳng song song với CD cắt BD tại Q. Ta có mp (MNPQ) song song với cả AB và CD. Từ đó
![]()
Áp dụng tính chất đường trung bình trong tam giác (do M, N là các trung điểm) ta suy ra được MP = MQ = NP = a hay tứ giác MPNQ là hình thoi.
Tính được