Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: AD=AC
a: Xét ΔACE và ΔADE có
AC=AD
\(\widehat{CAE}=\widehat{DAE}\)
AE chung
DO đó: ΔACE=ΔADE
Suy ra: \(\widehat{CAE}=\widehat{DAE}\)
hay AE là phân giác của góc CAB
b: Ta có: AC=AD
EC=ED
DO đó: AE là đường trung trực của CD
c: ta có: AE là đường trung trực của CD
nên AE\(\perp\)CD tại I
=>ΔAID vuông tại I
=>\(\widehat{ADI}< 90^0\)
=>\(\widehat{CDB}>90^0\)(Do góc ADI và góc CDB là hai góc kề bù)
Xét ΔCDB có \(\widehat{CDB}>90^0\)
nên BC là cạnh lớn nhất
=>BC>CD

Giả sử M(m;0) và N(0;n)
\(\overrightarrow{AM}\left(m-4;-1\right)\)
\(\overrightarrow{NO}\left(0;-n\right)\)
\(\)Vì \(\overrightarrow{AM}=\overrightarrow{NO}\rightarrow\left\{{}\begin{matrix}m=4\\n=1\end{matrix}\right.\)
Khi đó ta tìm được pt (d): x+4y-4=0

Đừng bao giờ hỏi em bài hình học:(( Nếu anh có tag thì tag em mấy bài BĐT, Hệ PT, PT á...
Phạm Hoàng Lê Nguyên đang học phần nào đấy ạ, nhìn như hàng điểm điều hòa, để em nghĩ với. từ giờ cứ tag em vào cho vui ^^

Đáp án A
Ta có 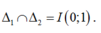
Vì A thuộc ∆1 nên A( a; a+ 1).
Vì P( 2;1) là trung điểm của đoạn AB nên B( 4-a; 1-a).
Mặt khác:
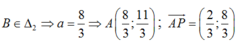
Đường thẳng AP có VTPT ( 4;-1) và qua P(2;1) nên có phương trình:
4x – y- 7 = 0

A B C K P Q M N
Áp dụng ĐL Melelaus có \(\frac{\overline{QB}}{\overline{QC}}.\frac{\overline{MA}}{\overline{MB}}.\frac{\overline{NC}}{\overline{NA}}=1\Rightarrow\frac{\overline{QB}}{\overline{QC}}=\frac{\overline{MB}}{\overline{MA}}.\frac{\overline{NA}}{\overline{NC}}\) (1)
Áp dụng ĐL Ceva có \(\frac{\overline{MB}}{\overline{MA}}.\frac{\overline{NA}}{\overline{NC}}.\frac{\overline{PC}}{\overline{PB}}=-1\Rightarrow\frac{\overline{PB}}{\overline{PC}}=-\frac{\overline{MB}}{\overline{MA}}.\frac{\overline{NC}}{\overline{NA}}\) (2)
Từ (1) và (2) suy ra \(\frac{\overline{PB}}{\overline{PC}}=-\frac{\overline{QB}}{\overline{QC}}\). Như vậy \(\left(BCPQ\right)=-1\)tức là hàng điều hòa (đpcm).
P/S: Đề bị thừa điểm O nhé bạn.
Cho mình sửa dòng thứ hai: \(\frac{\overline{PB}}{\overline{PC}}=-\frac{\overline{MB}}{\overline{MA}}.\frac{\overline{NA}}{\overline{NC}}\) mới đúng.