Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Xét △ AFC và △ AEB có:
\(\widehat{BAC}\) chung
\(\widehat{AFC}=\widehat{AEB}=90^0\)
⇒ △AFC đồng dạng với △ AEB(g.g)
⇒ \(\frac{AF}{AE}=\frac{AC}{AB}\)
⇒ \(AB.AF=AE.AC\)
\(\frac{AF}{AE}=\frac{AC}{AB}\Rightarrow\frac{AF}{AC}=\frac{AE}{AB}\)
Xét △ AEF và △ ABC có :
\(\widehat{BAC}\) chung
\(\frac{AF}{AC}=\frac{AE}{AB}\left(cmt\right)\)
⇒△ AEF đồng dạng với △ ABC (c.g.c)
Mấy câu kia bạn tự làm nốt đi nhá.
+) Câu d sửa đề thành BF . BA + CE . CA = BC2
a, Xét △AFH vuông tại F và △ADB vuông tại D
Có: FAH là góc chung
=> △AFH ᔕ △ADB (g.g)
b, Vì △AFH ᔕ △ADB (cmt) \(\Rightarrow\frac{AF}{AD}=\frac{AH}{AB}\)\(\Rightarrow\frac{AB}{AD}=\frac{AH}{AF}\)
Xét △ABH và △ADF
Có: \(\frac{AB}{AD}=\frac{AH}{AF}\)(cmt)
BAH là góc chung
=> △ABH ᔕ △ADF (c.g.c)
c, Xét △HFB vuông tại F và △HEC vuông tại E
Có: FHB = EHC (2 góc đối đỉnh)
=> △HFB ᔕ △HEC (g.g)
\(\Rightarrow\frac{HF}{HE}=\frac{HB}{HC}\)
=> HF . HC = HE . HB
d, Sửa đề thành BF . BA + CE . CA = BC2
Xét △HEC vuông tại E và △AFC vuông tại F
Có: HCE là góc chung
=> △HEC ᔕ △AFC (g.g)
\(\Rightarrow\frac{EC}{FC}=\frac{HC}{AC}\)
=> FC . HC = EC . AC (1)
Xét △HFB vuông tại F và △AEB vuông tại E
Có: FBH là góc chung
=> △HFB ᔕ △AEB (g.g)
\(\Rightarrow\frac{FB}{EB}=\frac{HB}{AB}\)
=> FB . AB = EB . HB (2)
Xét △BFC vuông tại F và △HDC vuông tại D
Có: HCD là góc chung
=> △BFC ᔕ △HDC (g.g)
\(\Rightarrow\frac{FC}{DC}=\frac{BC}{HC}\)
=> FC . HC = BC . DC (3)
Xét △BEC vuông tại E và △BDH vuông tại D
Có: HBD là góc chung
=> △BEC ᔕ △BDH (g.g)
\(\Rightarrow\frac{BC}{BH}=\frac{BE}{DB}\)
=> BC . DB = BE . BH (4)
Từ (1) và (3) => EC . AC = BC . DC
Từ (2) và (4) => FB . AB = BC . DB
Ta có: BF . BA + CE . CA = BC . BD + BC . DC = BC . (BD + DC) = BC . BC = BC2
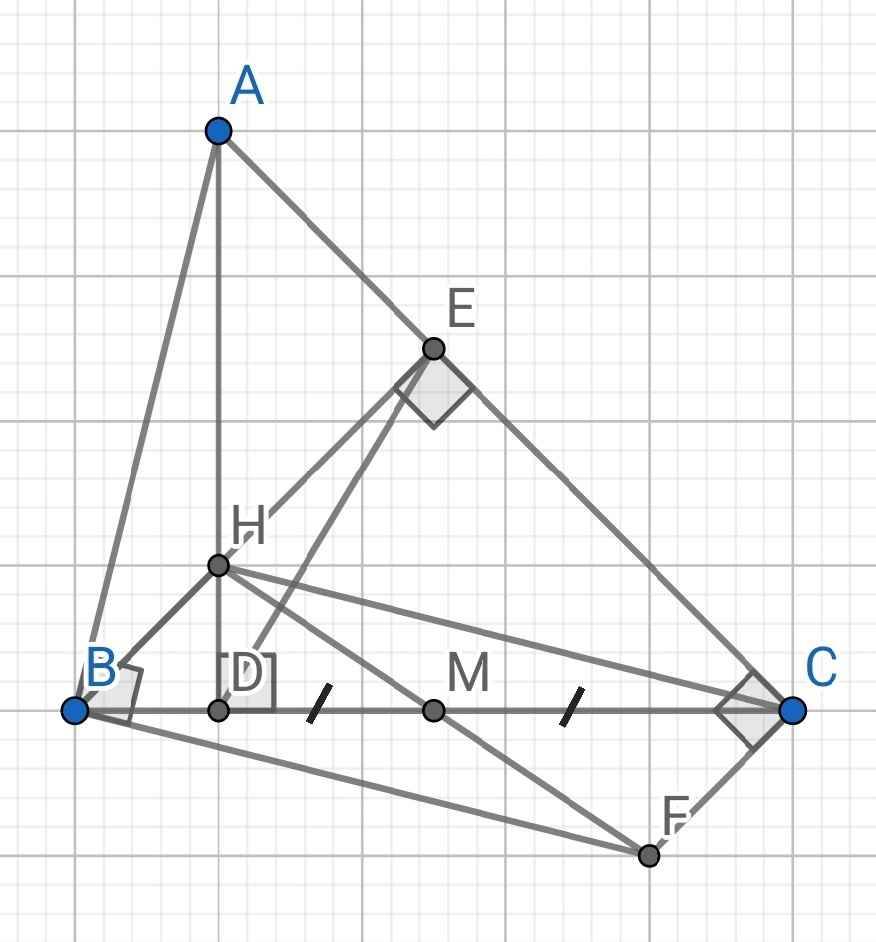d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
⇒ CH là đường cao thứ ba của ∆ABC
⇒ CH ⊥ AB
Mà BF ⊥ AB (gt)
⇒ CH // BF
Do CF ⊥ AC (gt)
BE ⊥ AC (gt)
⇒ CF // BE
⇒ CF // BH
Tứ giác BHCF có:
CH // BF (cmt)
CF // BH (cmt)
⇒ BHCF là hình bình hành
e) Do BHCF là hình bình hành (cmt)
Mà M là trung điểm của đường chéo BC (gt)
⇒ M là trung điểm của đường chéo HF
⇒ H, M, F thẳng hàng